题目内容
4.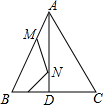 等边△ABC的边长是8,AD⊥BC,E是BD的中点,M、N分别是AB、AD上的动点,求MN+EN的最小值.
等边△ABC的边长是8,AD⊥BC,E是BD的中点,M、N分别是AB、AD上的动点,求MN+EN的最小值.
分析 作E关于AD的对称点E′,过E′作E′M⊥AB于M交AD于N,则MN+EN的最小值=E′M,根据等边三角形的性质得到BD=4,求得BE′=6,解直角三角形即可得到结论.
解答 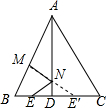 解:作E关于AD的对称点E′,过E′作E′M⊥AB于M交AD于N,
解:作E关于AD的对称点E′,过E′作E′M⊥AB于M交AD于N,
则MN+EN的最小值=E′M,
∵△ABC是等边三角形,AD⊥BC,BC=8,
∴BD=4,
∵E是BD的中点,
∴BE=DE=2,
∴BE′=6,
∵∠B=60°,∠BME′=90°,
∴ME′=3$\sqrt{3}$,
∴MN+EN的最小值是3$\sqrt{3}$.
点评 本题考查轴对称-最短路线问题、等边三角形的性质,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.下面哪个点在函数y=$\frac{1}{4}$x+1的图象上( )
| A. | (4,1) | B. | (-4,1) | C. | (4,0) | D. | (-4,0) |
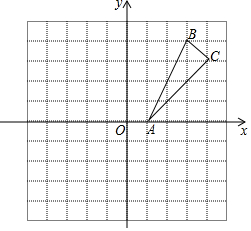 如图,在平面直角坐标系中,每一格表示1个单位长度,△ABC的三个顶点都在格点上;
如图,在平面直角坐标系中,每一格表示1个单位长度,△ABC的三个顶点都在格点上;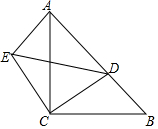 如图,等腰直角△ABC中,AC=BC,∠ACB=90°,点D为斜边AB上一点,若AB=14,BD=6,将△BCD绕点C逆时针方向旋转到△ACE的位置,对于下列说法:①△ADE是直角三角形,②△CDE是等腰三角形,③DE=10,④CD=5$\sqrt{2}$.其中正确说法是①②③④(填序号).
如图,等腰直角△ABC中,AC=BC,∠ACB=90°,点D为斜边AB上一点,若AB=14,BD=6,将△BCD绕点C逆时针方向旋转到△ACE的位置,对于下列说法:①△ADE是直角三角形,②△CDE是等腰三角形,③DE=10,④CD=5$\sqrt{2}$.其中正确说法是①②③④(填序号).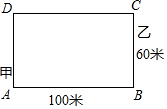 如图,有一条长方形跑道,甲从A点出发,乙从C点发.同时按逆时针方奔跑.甲速每秒6.25米,乙速每秒5米.跑道长100米,宽60米.当甲、乙每次跑道拐点A、B、C、D时都要停留5秒.问当甲第1次追上乙时,甲、乙各跑了多少米.
如图,有一条长方形跑道,甲从A点出发,乙从C点发.同时按逆时针方奔跑.甲速每秒6.25米,乙速每秒5米.跑道长100米,宽60米.当甲、乙每次跑道拐点A、B、C、D时都要停留5秒.问当甲第1次追上乙时,甲、乙各跑了多少米. 甲乙两种作物的单位面积的产量比是1:1.5,现在要在一块长为200m,宽100m的长方形的土地上种植这两种作物,怎样把这块地分为两个长方形,使甲乙两种作物的总产量比为3:4(结果取整数)?
甲乙两种作物的单位面积的产量比是1:1.5,现在要在一块长为200m,宽100m的长方形的土地上种植这两种作物,怎样把这块地分为两个长方形,使甲乙两种作物的总产量比为3:4(结果取整数)?