题目内容
3.解不等式组:$\left\{\begin{array}{l}4x+5≥1\\ \frac{1}{3}x+1>2(x-2)\end{array}\right.$并写出最小整数解.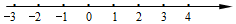
分析 分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
解答 解:由4x+5≥1得:x≥-1,
由$\frac{1}{3}$x+1>2(x-2)得:x<3.
所以原不等式组的解集为-1≤x<3.
因此原不等式组的最小整数解是-1.
点评 本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
相关题目
8.下列四个选项中,表示算式-5$\frac{3}{7}$+2计算结果,正确的是( )
| A. | $-5\frac{1}{7}$ | B. | $-3\frac{3}{7}$ | C. | $7\frac{3}{7}$ | D. | $-7\frac{3}{7}$. |
 如图所示,在△ABC中,∠A=70°,点D是BC延长线上的一点,∠ACD=150°,则∠B=80°.
如图所示,在△ABC中,∠A=70°,点D是BC延长线上的一点,∠ACD=150°,则∠B=80°.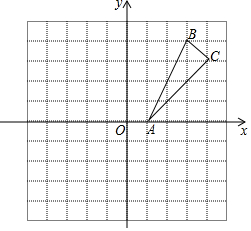 如图,在平面直角坐标系中,每一格表示1个单位长度,△ABC的三个顶点都在格点上;
如图,在平面直角坐标系中,每一格表示1个单位长度,△ABC的三个顶点都在格点上; 如图,BP是∠MBN的平分线,D是BP上一点,AD⊥BN于点A,AD=3,C是BM上的一点,BC=5,则△BCD的面积为( )
如图,BP是∠MBN的平分线,D是BP上一点,AD⊥BN于点A,AD=3,C是BM上的一点,BC=5,则△BCD的面积为( )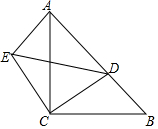 如图,等腰直角△ABC中,AC=BC,∠ACB=90°,点D为斜边AB上一点,若AB=14,BD=6,将△BCD绕点C逆时针方向旋转到△ACE的位置,对于下列说法:①△ADE是直角三角形,②△CDE是等腰三角形,③DE=10,④CD=5$\sqrt{2}$.其中正确说法是①②③④(填序号).
如图,等腰直角△ABC中,AC=BC,∠ACB=90°,点D为斜边AB上一点,若AB=14,BD=6,将△BCD绕点C逆时针方向旋转到△ACE的位置,对于下列说法:①△ADE是直角三角形,②△CDE是等腰三角形,③DE=10,④CD=5$\sqrt{2}$.其中正确说法是①②③④(填序号). 甲乙两种作物的单位面积的产量比是1:1.5,现在要在一块长为200m,宽100m的长方形的土地上种植这两种作物,怎样把这块地分为两个长方形,使甲乙两种作物的总产量比为3:4(结果取整数)?
甲乙两种作物的单位面积的产量比是1:1.5,现在要在一块长为200m,宽100m的长方形的土地上种植这两种作物,怎样把这块地分为两个长方形,使甲乙两种作物的总产量比为3:4(结果取整数)?