题目内容
1.阅读下面材料:小明通过这样一个问题:如图(1),已知等腰三角形ABC,AB=AC.求作一个正方形,使得正方形的两个顶点在BC上,其余两个顶点分别在AB和AC上.
小明发现,以BC为边在△ABC的另一侧作正方形BCEF,连接AE交DC于点G,连接AF与BC交于点H,过H作BF的平行线交AB于点N,过G作CE的平行线交AC于点M,连接MN,易证$\frac{NH}{BF}=\frac{HG}{FE}=\frac{GM}{CE}$,经过进一步推理可以说明四边形GHNM是正方形,如图(2).
(1)请回答:若AB=AC=5,∠BAC=90°,则正方形GHNM的面积为$\frac{50}{9}$;
(2)参考小明思考问题的方法,解决问题:如图(3),已知△ABC,求作等边三角形DEF,使得点D、E、F分别在△ABC的三条边上.
要求:使用尺规作图,不写作法,但保留作图痕迹.

分析 (1)易证△BHN和△CGM是等腰直角三角形,从而可证到BH=GH=CG,只需求出BC的值,就可解决问题;
(2)分别以点B、C为圆心,BC为半径画弧,在△ABC的另一侧交于点G,连接AG交BC于点D,作∠ADF=∠AGB,交AB于点F,作∠ADE=∠AGC,交AC于点E,连接EF,△DEF即为所求作.
解答 解:(1)如图(2),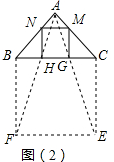
∵AB=AC=5,∠BAC=90°,
∴∠ABC=∠ACB=45°,BC=5$\sqrt{2}$.
∵四边形GHNM是正方形,
∴NH=HG=MG,∠NHG=∠HGM=90°,
∴∠BNH=∠CMG=45°,
∴∠ABC=∠ACB=∠BNH=∠CMG,
∴BH=NH,CG=MG,
∴BH=GH=CG,
∴BC=3GH=5$\sqrt{2}$,
∴GH=$\frac{5\sqrt{2}}{3}$,
∴正方形GHNM的面积为$\frac{50}{9}$.
故答案为$\frac{50}{9}$;
(2)如图3,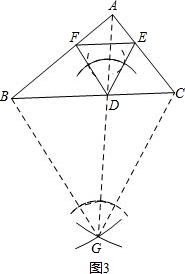
△DEF即为所求作.
注:不写结论要扣分.
点评 本题主要考查了等腰直角三角形的判定与性质、正方形的性质、勾股定理等知识,另外还考查了运用尺规作等边三角形和平行线,把作平行线转化为作一个角等于已知角是解决第(2)小题的关键,需要注意的是作出图形后要下结论.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
11.下面给出了6个式子:
①3>0;②4x+3y>0;③x=3;④x-1;⑤x+2≤3;⑥2x≠0.
其中不等式有( )
①3>0;②4x+3y>0;③x=3;④x-1;⑤x+2≤3;⑥2x≠0.
其中不等式有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
12.己知反比例函数y=$\frac{6}{x}$,当1<x<3时,y的取值范围是( )
| A. | 0<y<l | B. | 1<y<2 | C. | y>6 | D. | 2<y<6 |
10.有一箱子装有3张分别标示4、5、6的号码牌,已知小南以每次取一张且取后不放回的方式,先后取出2张牌,组成一个两位数,取出第1张牌的号码为十位数,第2张牌的号码为个位数,则组成的二位数为5的倍数的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
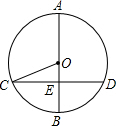 如图,⊙O中直径AB⊥弦CD于E,若AB=26,CD=24,则OE=5.
如图,⊙O中直径AB⊥弦CD于E,若AB=26,CD=24,则OE=5.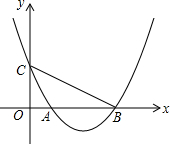 如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c与x轴交于A(1,0),B(4,0)两点,与y轴交于点C(0,2).
如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c与x轴交于A(1,0),B(4,0)两点,与y轴交于点C(0,2).