题目内容
 如图,在△ABC中,AB=AC,∠BAC=120°,D为BC中点,DE⊥AB于E,AD=4,求线段BE的长度.
如图,在△ABC中,AB=AC,∠BAC=120°,D为BC中点,DE⊥AB于E,AD=4,求线段BE的长度.考点:含30度角的直角三角形,等腰三角形的性质
专题:
分析:根据等腰三角形两底角相等求出∠B=30°,根据等腰三角形三线合一的性质可得AD⊥BC,然后求出∠ADE=30°,再根据直角三角形30°角所对的直角边等于斜边的一半求出AE、AB,然后根据BE=AB-AE计算即可得解.
解答:解:∵AB=AC,∠BAC=120°,
∴∠B=
×(180°-120°)=30°,
∵AB=AC,D为BC中点,
∴AD⊥BC,
∵DE⊥AB,
∴∠ADE=∠B=30°,
∴AE=
AD=
×4=2,
AB=2AD=2×4=8,
∴BE=AB-AE=8-2=6.
∴∠B=
| 1 |
| 2 |
∵AB=AC,D为BC中点,
∴AD⊥BC,
∵DE⊥AB,
∴∠ADE=∠B=30°,
∴AE=
| 1 |
| 2 |
| 1 |
| 2 |
AB=2AD=2×4=8,
∴BE=AB-AE=8-2=6.
点评:本题考查了直角三角形30°角所对的直角边等于斜边的一半的性质,等腰三角形三线合一的性质,等腰三角形两底角相等的性质,熟记各性质并准确识图是解题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
可以由抛物线y=x2平移得到抛物线y=(x-2)2+1,下列平移方法中正确的是( )
| A、向右平移2个单位,再向上平移1个单位 |
| B、向右平移2个单位,再向下平移1个单位 |
| C、向左平移2个单位,再向上平移1个单位 |
| D、向左平移2个单位,再向下平移1个单位 |
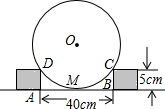 如图,为了测量圆形工件的直径,在工作台上用边长都为5cm的两个立方体小木块顶在圆形工件的两侧,测得两木块间的距离AB=40cm.
如图,为了测量圆形工件的直径,在工作台上用边长都为5cm的两个立方体小木块顶在圆形工件的两侧,测得两木块间的距离AB=40cm. 如图,BD是∠ABC的角平分线,DE⊥AB于E,△ABC的面积是60,AB=18,BC=12,则DE=
如图,BD是∠ABC的角平分线,DE⊥AB于E,△ABC的面积是60,AB=18,BC=12,则DE=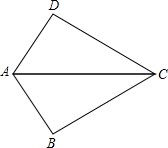 如图,已知AB=AD,那么添加下列一个条件后,能用SAS判定△ABC≌△ADC的是
如图,已知AB=AD,那么添加下列一个条件后,能用SAS判定△ABC≌△ADC的是