题目内容
19．一元二次方程x（x-3）=3-x的根是（ ）| A． | x=-1 | B． | x=3 | C． | x1=-1，x2=3 | D． | x1=1，x2=2 |
分析 移项，分解因式，即可得出两个一元一次方程，求出方程的解即可．
解答 解：x（x-3）=3-x，
x（x-3）+（x-3）=0
（x-3）（x+1）=0
x+1=0，x-3=0，
x1=-1，x2=3．
故选C．
点评 本题考查了解一元二次方程的应用，能把一元二次方程转化成一元一次方程是解此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，直线a∥b，∠1=115°，求∠2的度数．
14．如果一个三角形的外角平分线与这个三角形一边平行，则这个三角形一定是（ ）
| A． | 锐角三角形 | B． | 等腰三角形 | C． | 等边三角形 | D． | 等腰直角三角形 |
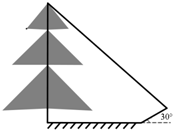某同学测量一棵树的高度，某时刻树的影子恰好落在地面和一斜坡上，如图，此时测得地面上的影长为6米，坡面上的影长为4米，一直斜坡的坡角为30°，同一时刻，一根长为3米，垂直于地面放置的标杆在地面上的影长为1.5米，则树的高度为（14+4$\sqrt{3}$）米．
8．下列各式中，正确的是（ ）
| A． | $\frac{-x+y}{-x-y}$=$\frac{x-y}{x+y}$ | B． | $\frac{-x+y}{x-y}$=$\frac{-x-y}{x-y}$ | C． | $\frac{-x+y}{-x-y}$=$\frac{x+y}{x-y}$ | D． | $\frac{-x+y}{x-y}$=$\frac{x-y}{x+y}$ |