题目内容
 如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于E,垂足为D,若BD=5,则CE的长为
如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于E,垂足为D,若BD=5,则CE的长为考点:含30度角的直角三角形,线段垂直平分线的性质
专题:
分析:在Rt△BDE中可得到BE=2DE,根据勾股定理可求得DE,可求得BE的长,根据线段垂直平分线的性质可求得CE的长.
解答:解:
∵DE垂直平分BC,
∴CE=BE,∠EDB=90°,
∵∠B=30°,
∴BE=2DE,
在Rt△BDE中,由勾股定理可得BE2=DE2+BD2,
即4DE2=DE2+52,解得DE=
,
∴CE=BE=2DE=
,
故答案为:
.
∵DE垂直平分BC,
∴CE=BE,∠EDB=90°,
∵∠B=30°,
∴BE=2DE,
在Rt△BDE中,由勾股定理可得BE2=DE2+BD2,
即4DE2=DE2+52,解得DE=
5
| ||
| 3 |
∴CE=BE=2DE=
10
| ||
| 3 |
故答案为:
10
| ||
| 3 |
点评:本题主要考查线段垂直平分线的性质及直角三角形的性质,掌握直角三角形中30°角所对的直角边是斜边的一半是解题的关键

练习册系列答案
相关题目
已知甲、乙两坡的倾斜角分别为α、β,若甲坡比乙坡陡,则下列选项成立的是( )
| A、cosα<cosβ |
| B、cosα>cosβ |
| C、sinα<sinβ |
| D、tanα<tanβ |
 在△ABC中,∠ACB=90°,∠A=30°,CD⊥AB.
在△ABC中,∠ACB=90°,∠A=30°,CD⊥AB.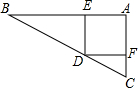 如图,一个直角三角形的苗圃由正方形花坛和两块直角三角形的草皮组成,两个直角三角形的斜边长分别为3m和6m.
如图,一个直角三角形的苗圃由正方形花坛和两块直角三角形的草皮组成,两个直角三角形的斜边长分别为3m和6m. 如图,在Rt△ABC中,CD是斜边AB上的中线,已知CD=5,AC=6,则BC的长等于
如图,在Rt△ABC中,CD是斜边AB上的中线,已知CD=5,AC=6,则BC的长等于