题目内容
10.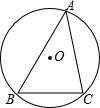 如图,⊙O是△ABC的外接圆,⊙O的半径为4,∠A=45°,则$\widehat{BC}$的长是( )
如图,⊙O是△ABC的外接圆,⊙O的半径为4,∠A=45°,则$\widehat{BC}$的长是( )| A. | 4π | B. | 8π | C. | 2π | D. | 1 |
分析 连接OB、OC,根据圆周角定理求出∠BOC,利用弧长公式计算即可.
解答 解:连接OB、OC,
由圆周角定理得,∠BOC=2∠A=90°,
∴$\widehat{BC}$的长=$\frac{90π×4}{180}$=2π,
故选:C.
点评 本题考查的是三角形的外接圆和外心的概念和性质,掌握圆周角定理、弧长公式是解题的关键.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
20.下列命题是假命题的是( )
| A. | 两组对边分别平行的四边形是平行四边形 | |
| B. | 两条对角线相等的平行四边形是矩形 | |
| C. | 两条对角线互相垂直的平行四边形是菱形 | |
| D. | 两条对角线垂直且相等的四边形是正方形 |
1.a、b是两个连续整数,若a<$\sqrt{3}$<b,则a、b分别是( )
| A. | 0、1 | B. | 1、2 | C. | 2、3 | D. | 3、4 |
2.已知P1(x1,y1),P2(x2,y2)是一次函数y=-$\frac{1}{3}$x+2图象上的两点,下列判断中,正确的是( )
| A. | y1>y2 | B. | y1<y2 | C. | 当x1<x2时,y1<y2 | D. | 当x1<x2时,y1>y2 |
 如图,PA、PB是⊙O的两条切线,A、B是切点,PA=$\sqrt{3}$OA,阴影部分的面积为6π,则⊙O的半径长为3.
如图,PA、PB是⊙O的两条切线,A、B是切点,PA=$\sqrt{3}$OA,阴影部分的面积为6π,则⊙O的半径长为3.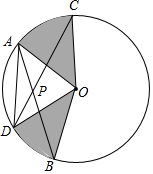 如图,⊙O的两条弦AB、CD相交于点P,∠APC=45°,若⊙O的半径为4,则扇形AOC与扇形DOB面积(图中阴影部分)的和为4π.
如图,⊙O的两条弦AB、CD相交于点P,∠APC=45°,若⊙O的半径为4,则扇形AOC与扇形DOB面积(图中阴影部分)的和为4π.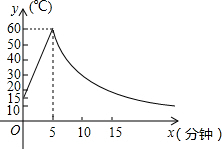 制作一种产品,需先将材料加热达到60℃后,再进行操作.设该材料温度为y(℃),从加热开始计算的时间为x(分钟).据了解,设该材料加热时,温度y与时间x成一次函数关系;停止加热进行操作时,温度y与时间x成反比例关系(如图).已知该材料在操作加工前的温度为15℃,加热5分钟后温度达到60℃.
制作一种产品,需先将材料加热达到60℃后,再进行操作.设该材料温度为y(℃),从加热开始计算的时间为x(分钟).据了解,设该材料加热时,温度y与时间x成一次函数关系;停止加热进行操作时,温度y与时间x成反比例关系(如图).已知该材料在操作加工前的温度为15℃,加热5分钟后温度达到60℃.