题目内容
15.(1)计算:2cos45°-$\sqrt{8}$+(2018-$\sqrt{2017}$)0(2)化简:1-$\frac{a-1}{a}$÷$\frac{{a}^{2}-1}{{a}^{2}+2a}$.
分析 (1)根据特殊角的三角函数值和零指数幂可以解答本题;
(2)根据分式的除法和减法可以解答本题.
解答 解:(1)2cos45°-$\sqrt{8}$+(2018-$\sqrt{2017}$)0
=2×$\frac{\sqrt{2}}{2}$-2$\sqrt{2}$+1
=$\sqrt{2}-2\sqrt{2}+1$
=$-\sqrt{2}$+1;
(2)1-$\frac{a-1}{a}$÷$\frac{{a}^{2}-1}{{a}^{2}+2a}$
=1-$\frac{a-1}{a}×\frac{a(a+2)}{(a+1)(a-1)}$
=1-$\frac{a+2}{a+1}$
=$\frac{a+1-a-2}{a+1}$
=$-\frac{1}{a+1}$.
点评 本题考查分式的混合运算、实数的运算、零指数幂、特殊角的三角函数值,解答本题的关键是明确它们各自的计算方法.

练习册系列答案
相关题目
5.-($\frac{1}{2}$)-2的倒数是( )
| A. | -4 | B. | $-\frac{1}{4}$ | C. | $\frac{1}{4}$ | D. | 4 |
6.若代数式$\frac{1}{x+3}$在实数范围内有意义,则实数x的取值范围是( )
| A. | x≠-3 | B. | x=-3 | C. | x<-3 | D. | x>-3 |
10.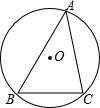 如图,⊙O是△ABC的外接圆,⊙O的半径为4,∠A=45°,则$\widehat{BC}$的长是( )
如图,⊙O是△ABC的外接圆,⊙O的半径为4,∠A=45°,则$\widehat{BC}$的长是( )
 如图,⊙O是△ABC的外接圆,⊙O的半径为4,∠A=45°,则$\widehat{BC}$的长是( )
如图,⊙O是△ABC的外接圆,⊙O的半径为4,∠A=45°,则$\widehat{BC}$的长是( )| A. | 4π | B. | 8π | C. | 2π | D. | 1 |
20.下列运算正确的是( )
| A. | a6+a3=a9 | B. | a2•a3=a5 | C. | (2a)3=6a3 | D. | (a-b)2=a2-b2 |
4.若关于x的方程x2+bx+1=0有两个不相等的实数根,则a的值可以是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
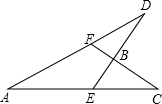 如图所示,已知∠A=27°,∠CBE=90°,∠C=30°,则∠D的度数为33度.
如图所示,已知∠A=27°,∠CBE=90°,∠C=30°,则∠D的度数为33度.