题目内容
20.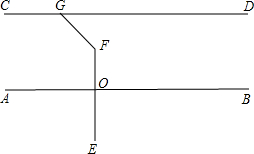 如图:已知AB∥CD,EF⊥AB于点O,∠FGC=131°,求∠EFG的度数.
如图:已知AB∥CD,EF⊥AB于点O,∠FGC=131°,求∠EFG的度数.下面提供三种思路:
(1)过点F作FH∥AB;
(2)延长EF交CD于M;
(3)延长GF交AB于K.
请你利用三个思路中的两个思路,将图形补充完整,求∠EFG的度数.
解(一):
解(二):
分析 (1)由EF⊥AB可得出∠BOF=90°,根据“平行于同一条直线的两直线互相平行”可得出FH∥CD,由“两直线平行,同旁内角互补”可得出∠GFH=49°,进而即可求出∠EFG的度数;
(2)由EF⊥AB可得出∠BOF=90°,由“两直线平行,内错角相等”可得出∠GMF=∠BOF=90°,利用邻补角互补可求出∠FGM=49°,再根据三角形内角和定理可求出∠MFG=41°,结合邻补角互补可求出∠EFG的度数;
(3)由EF⊥AB可得出∠KOF=90°,由“两直线平行,同旁内角互补”可得出∠FKO=49°,利用三角形内角和定理可得出∠OFK=41°,再利用邻补角互补可求出∠EFG的度数.
解答 解(一):利用思路(1)过点F 作FH∥AB,如图1所示.
∵EF⊥AB,
∴∠BOF=90°.
∵FH∥AB,AB∥CD,
∴FH∥CD.
∵∠FGC+∠GFH=180°,∠FGC=131°,
∴∠GFH=49°,
∴∠GFO=∠GFH+∠HFO=49°+90°=139°.
解(二):利用思路(2)延长EF交CD于M,如图2所示.
∵EF⊥AB,
∴∠BOF=90°.
∵AB∥CD,
∴∠GMF=∠BOF=90°.
∵∠FGC=131°,
∴∠FGM=49°.
∵∠FGM+∠GMF+∠MFG=180°,
∴49°+90°+∠MFG=180°,
∴∠MFG=41°,
∴∠GFO=180°-∠MFG=139°.
解(三):利用思路(3)延长GF交AB于K,如图3所示.
∵EF⊥AB,
∴∠KOF=90°.
∵CD∥AB,
∴∠FKO+∠FGC=180°.
∵∠FGC=131°,
∴∠FKO=49°.
∵∠FKO+∠KOF+∠OFK=180°,
∴49°+90°+∠OFK=180°,
∴∠OFK=41°,
∴∠GFO=180°-∠OFK=139°.
点评 本题考查了平行线的性质、垂线以及三角形内角和定理,解题的关键是:(1)利用“两直线平行,同旁内角互补”得出∠GFH的度数;(2)利用三角形内角和定理求出∠MFG的度数;(3)利用三角形内角和定理求出∠OFK的度数.

 尺规作图:用直尺和圆规作图,不写作法,保留痕迹.
尺规作图:用直尺和圆规作图,不写作法,保留痕迹.
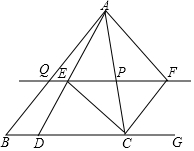 如图,在△ABC 中,点P是AC边上的一点,过点P作与BC平行的直线PQ,交AB于点Q,点D在线段 BC上,联接AD交线段PQ于点E,且$\frac{CP}{CD}$=$\frac{QE}{BD}$,点G在BC延长线上,∠ACG的平分线交直线PQ于点F.
如图,在△ABC 中,点P是AC边上的一点,过点P作与BC平行的直线PQ,交AB于点Q,点D在线段 BC上,联接AD交线段PQ于点E,且$\frac{CP}{CD}$=$\frac{QE}{BD}$,点G在BC延长线上,∠ACG的平分线交直线PQ于点F.