��Ŀ����
15�� ��ABCΪ�߳�2���������Σ��Ե�AΪԲ�ģ�lΪ�뾶��Բ����AB��AC����E��F���㣬��P��$\widehat{EF}$�Ķ��㣬����AP�����ӳ����߶�BC�ڵ�K������P��������Բ�����ߣ��������߲���BCƽ��ʱ��������ֱ��BC���ڵ�M��
��ABCΪ�߳�2���������Σ��Ե�AΪԲ�ģ�lΪ�뾶��Բ����AB��AC����E��F���㣬��P��$\widehat{EF}$�Ķ��㣬����AP�����ӳ����߶�BC�ڵ�K������P��������Բ�����ߣ��������߲���BCƽ��ʱ��������ֱ��BC���ڵ�M����1����K��B�غ�ʱ��PM��KP��ֵ�Ƕ��٣�
��2���ڵ�P�˶��Ĺ����У��Ƿ����PM��KP=3������������ڣ������BK��ֵ���������ڣ���˵�����ɣ�
��3��һ��أ��Ƿ����PM��KP=n��nΪ����������������������IJ��루��Ҫ��֤����
���� ��1����ͼ1�У���K��B�غ�ʱ��P��E�غϣ�M��C�غϣ��ɴ˲��ѽ�����⣮
��2����ͼ2�У���AD��BC��D���ɡ�ADK�ס�MPK���Ƴ�$\frac{AD}{KD}$=$\frac{PM}{PK}$=3���ɴ˲��ѽ�����⣬ע�AK��AD�Ҳ�ʱ���������ƣ�
��3���������ƣ�2����
��� ��1���⣺��ͼ1�У���K��B�غ�ʱ��P��E�غϣ�M��C�غϣ�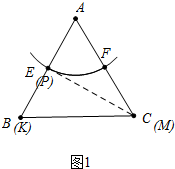
��$\frac{PM}{PK}$=tan60��=$\sqrt{3}$��
��PM��PK=$\sqrt{3}$��
��2�����ڣ�
���ɣ���ͼ2�У���AD��BC��D��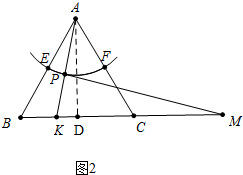
��MP�ǡ�A���ߣ�
���ADK=��MPK=90�㣬
�ߡ�AKD=��PKM��
���ADK�ס�MPK��
��$\frac{AD}{KD}$=$\frac{PM}{PK}$=3��
�ߡ�ABC�ǵȱ������Σ�AB=2��
��AD=$\sqrt{3}$��
��KD=$\frac{\sqrt{3}}{3}$��
��BK=1-$\frac{\sqrt{3}}{3}$��
��AK��AD�Ҳ�ʱ��BK=1+$\frac{\sqrt{3}}{2}$��
��3�����ڣ�
���ɣ��ɣ�2����֪����ADK�ס�MPK��
��$\frac{AD}{KD}$=$\frac{PM}{PK}$=n��
�ߡ�ABC�ǵȱ������Σ�AB=2��
��AD=$\sqrt{3}$��
��KD=$\frac{\sqrt{3}}{n}$��
��BK=1-$\frac{\sqrt{3}}{n}$��
��AK��AD�Ҳ�ʱ��BK=1+$\frac{\sqrt{3}}{n}$��
���� ���⿼��Բ�ۺ��⡢������Ǻ��������������ε��ж������ʣ��ȱ������ε����ʵ�֪ʶ������ؼ���ѧ�����ӳ��ø����ߣ��������������ν�����⣬�����п�ѹ���⣮

 ȫ�ų��100��ϵ�д�
ȫ�ų��100��ϵ�д� Ӣ�ŵ��ϵ�д�
Ӣ�ŵ��ϵ�д� ������������Ծ�ϵ�д�
������������Ծ�ϵ�д�| A�� | 18cm | B�� | 20 cm | C�� | 24 cm | D�� | 25cm |
| A�� | 3$\frac{1}{3}$ | B�� | -$\frac{3}{10}$ | C�� | $\frac{3}{10}$ | D�� | -$\frac{10}{3}$ |
| A�� | a+4��b+4 | B�� | 2a��2b | C�� | -2a��-2b | D�� | a-b��0 |
 ��ͼ����֪AB�ǡ�O��ֱ������CD��AB��E������BC��BD��AC�������н����в�һ����ȷ���ǣ�������
��ͼ����֪AB�ǡ�O��ֱ������CD��AB��E������BC��BD��AC�������н����в�һ����ȷ���ǣ�������| A�� | ��ACB=90�� | B�� | DE=CE | C�� | OE=BE | D�� | ��ACE=��ABC |
| A�� | -1 | B�� | 0 | C�� | $-\frac{3}{2}$ | D�� | �� |
| A�� | 2 | B�� | -2 | C�� | ��2 | D�� | 0 |