题目内容
1. 阅读理解题
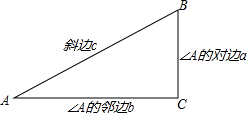
阅读理解题如图在Rt△ABC中,∠C=90°,我们把∠A的对边与斜边的比叫做∠A的正弦,记作sinA,即sinA=$\frac{∠A的对边}{斜边}$=$\frac{a}{c}$.把∠A的邻边与斜边的比叫做∠A的余弦.记作cosA,即cosA=$\frac{∠A的邻边}{斜边}$=$\frac{b}{c}$.把∠A的对边与∠A的邻边的比叫做∠A的正切,记作tanA,即tanA=$\frac{∠A的对边}{∠A的邻边}$=$\frac{a}{b}$.例如:在Rt△ABC中∠C=90°,a=8,b=15求sinA,cosA,tanA.
解:由勾股定理得:c=$\sqrt{{a^2}+{b^2}}$=$\sqrt{{8^2}+{{15}^2}}$=17,则:sinA=$\frac{a}{c}$=$\frac{8}{17}$cosA=$\frac{b}{c}$=$\frac{15}{17}$tanA=$\frac{a}{b}$=$\frac{8}{15}$
回答下列问题.
(1)在Rt△ABC中,AC=5,BC=12则:sinA=$\frac{12}{13}$,cosA=$\frac{5}{13}$,tanA=$\frac{12}{5}$.
(2)探索发现:①如(sinA)2简写成sin2A,(cosA)2简写成cos2A.则:sin2A+cos2A=1
②你能直接写出sinA,cosA,tanA三个量之间的一个等量关系号?答:tanA=$\frac{sinA}{cosA}$
(3)如果sinA=$\frac{3}{5}$,则tanA=$\frac{3}{4}$.
分析 (1)首先根据勾股定理计算出BC的长,再根据三角函数的定义分别计算出答案即可;
(2)根据三角函数的定义代入化简即可;
(3)根据题意,由sinα=$\frac{3}{5}$易得cosα的值,进而由同角三角函数的关系,求解可得答案.
解答 解:(1)在Rt△ABC中,AC=5,BC=12,
由勾股定理得AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{1{2}^{2}+{5}^{2}}$=13,
∴sinA=$\frac{BC}{AB}$=$\frac{12}{13}$,cosA=$\frac{AC}{AB}$=$\frac{5}{13}$,tanA=$\frac{BC}{AC}$=$\frac{12}{5}$;
故答案为:$\frac{12}{13}$,$\frac{5}{13}$,$\frac{12}{5}$;
(2)①∵sinA=$\frac{a}{c}$,cosA=$\frac{b}{c}$,
∴sin2A+cos2A=($\frac{a}{c}$)2+($\frac{b}{c}$)2=$\frac{{a}^{2}+{b}^{2}}{{c}^{2}}$=1;
故答案为:1;
②∵sinA=$\frac{a}{c}$,cosA=$\frac{b}{c}$,
∴tanA=$\frac{a}{b}$=$\frac{\frac{a}{c}}{\frac{b}{c}}$=$\frac{sinA}{cosA}$,
故答案为:tanA=$\frac{sinA}{cosA}$;
(3)∵sinA=$\frac{3}{5}$,
∴cosA=$\sqrt{1-(\frac{3}{5})^{2}}$=$\frac{4}{5}$,
∴tanA═$\frac{sinA}{cosA}$=$\frac{\frac{3}{5}}{\frac{4}{5}}$=$\frac{3}{4}$.
故答案为:$\frac{3}{4}$.
点评 本题考查锐角三角函数的定义及运用:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.

| A. | (-2)+(+2)=0 | B. | (-6)+(+4)=-10 | C. | 0+(-3)=-3 | D. | (+$\frac{5}{6}$)+(-$\frac{1}{6}$)=$\frac{2}{3}$ |
| A. | (-a,b) | B. | (a,-b) | C. | (-a,-b) | D. | (-b,-a) |
| A. | 全体整数 | B. | 全体实数 | C. | 全体有理数 | D. | 全体无理数 |
 .
.