题目内容
13.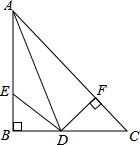 如图,AD为∠BAC的平分线,DF⊥AC于F,∠B=90°,DE=DC,试说明:BE=CF.
如图,AD为∠BAC的平分线,DF⊥AC于F,∠B=90°,DE=DC,试说明:BE=CF.
分析 先由角平分线的性质就可以得出DB=DF,再证明△BDE≌△FDC就可以求出结论.
解答 解:∵∠B=90°,
∴BD⊥AB.
∵AD为∠BAC的平分线,且DF⊥AC,
∴DB=DF.
在Rt△BDE和Rt△FDC中,
$\left\{\begin{array}{l}{DE=DC}\\{DB=DF}\end{array}\right.$,
∴Rt△BDE≌Rt△FDC(HL),
∴BE=CF.
点评 本题考查了角平分线的性质的运用,全等三角形的判定与性质的运用,解答时证明三角形全等是关键.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
3.大于1的正整数m的三次幂可“分裂”成若干个连续奇数的和,如:23=3+5,33=7+9+11,43=13+15+17+19,…,若m3按以上规律“分裂”后,其中有一个奇数是2017,则2017在若干个连续奇数中的位置是多少位( )
| A. | 16 | B. | 17 | C. | 18 | D. | 19 |
1.下列各式由左边到右边的变形中,是因式分解的是( )
| A. | a2-3a+2=a(a-3) | B. | a2x-a=a(ax-1) | C. | x2+3x+9=(x+3)2 | D. | (x+1)(x-1)=x2-1 |
18.今天教室温度是8℃,室外温度是零下6℃,则室内外温差( )
| A. | 2℃ | B. | 12℃ | C. | 14℃ | D. | 16℃ |
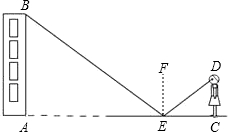 小红用下面的方法来测量学校教学大楼AB的高度:如图,在水平地面点E处放一面平面镜,镜子与教学大楼的距离AE=20m.当她与镜子的距离CE=2.5m时,她刚好能从镜子中看到教学大楼的顶端B.已知她的眼睛距地面高度DC=1.5m,请你帮助小红计算大楼的高度.
小红用下面的方法来测量学校教学大楼AB的高度:如图,在水平地面点E处放一面平面镜,镜子与教学大楼的距离AE=20m.当她与镜子的距离CE=2.5m时,她刚好能从镜子中看到教学大楼的顶端B.已知她的眼睛距地面高度DC=1.5m,请你帮助小红计算大楼的高度.