题目内容
5.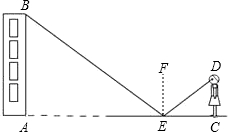 小红用下面的方法来测量学校教学大楼AB的高度:如图,在水平地面点E处放一面平面镜,镜子与教学大楼的距离AE=20m.当她与镜子的距离CE=2.5m时,她刚好能从镜子中看到教学大楼的顶端B.已知她的眼睛距地面高度DC=1.5m,请你帮助小红计算大楼的高度.
小红用下面的方法来测量学校教学大楼AB的高度:如图,在水平地面点E处放一面平面镜,镜子与教学大楼的距离AE=20m.当她与镜子的距离CE=2.5m时,她刚好能从镜子中看到教学大楼的顶端B.已知她的眼睛距地面高度DC=1.5m,请你帮助小红计算大楼的高度.
分析 根据反射定律和垂直定义得到∠BAE=∠DCE,所以可得△BAE∽△DCE,再根据相似三角形的性质解答.
解答  解:如图,
解:如图,
∵根据反射定律知:∠FEB=∠FED,
∴∠BEA=∠DEC
∵∠BAE=∠DCE=90°
∴△BAE∽△DCE
∴$\frac{AB}{DC}$=$\frac{AE}{EC}$,
∵CE=2.5米,DC=1.5米,
∴$\frac{AB}{1.5}$=$\frac{20}{2.5}$,
∴AB=12
∴大楼AB的高为12米.
点评 本题考查相似三角形性质的应用.解题时关键是找出相似的三角形,然后根据对应边成比例列出方程,建立适当的数学模型来解决问题.

练习册系列答案
相关题目
20.点A在y轴的右侧,x轴的下方,距离每个坐标轴都是2个单位长度,则点A的坐标是( )
| A. | (2,2) | B. | (-2,2) | C. | (-2,-2) | D. | (2,-2) |
17.在-2.5、+$\frac{7}{10}$、-3、2、0、4、5、-1 中,负分数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 0个 |
15. 如图,下列说法正确的是( )
如图,下列说法正确的是( )
 如图,下列说法正确的是( )
如图,下列说法正确的是( )| A. | 直线OM与直线MN是同一条直线 | B. | 射线MO与射线MN是同一条射线 | ||
| C. | 线段OM与线段ON是同一条线段 | D. | 射线NO与射线MO是同一条射线 |
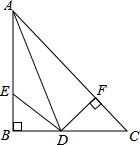 如图,AD为∠BAC的平分线,DF⊥AC于F,∠B=90°,DE=DC,试说明:BE=CF.
如图,AD为∠BAC的平分线,DF⊥AC于F,∠B=90°,DE=DC,试说明:BE=CF.