题目内容
3.已知:如图,在△ABC中,AB=AC,AD⊥BC于D,BE⊥AC于E,交AD于H点,在底边BC保持不变的情况下,当高AD变长或变短时,△ABC和△HBC的面积的积S△ABC,S△HBC的值是否随着变化?请说明你的理由.
分析 根据三角形的面积公式即可得到即可.
解答 解:变化,
理由:∵S△ABC=$\frac{1}{2}$BC•AD,
∴高AD变长或变短时,S△ABC将随着变大或变小,
∵S△HBC=$\frac{1}{2}$BC•DH,
∵DH随着高AD变长或变短也发生变化,
∴S△HBC的值随着变化.
点评 本题考查了三角形的面积公式,熟练掌握三角形的面积公式是解题的关键.

练习册系列答案
相关题目
15. 如图,下列说法正确的是( )
如图,下列说法正确的是( )
 如图,下列说法正确的是( )
如图,下列说法正确的是( )| A. | 直线OM与直线MN是同一条直线 | B. | 射线MO与射线MN是同一条射线 | ||
| C. | 线段OM与线段ON是同一条线段 | D. | 射线NO与射线MO是同一条射线 |
5.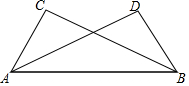 如图,△ABC≌△BAD,A和B,C和D是对应顶点,如果AB=6cm,BD=4cm,AD=5cm,那么BC等于( )
如图,△ABC≌△BAD,A和B,C和D是对应顶点,如果AB=6cm,BD=4cm,AD=5cm,那么BC等于( )
 如图,△ABC≌△BAD,A和B,C和D是对应顶点,如果AB=6cm,BD=4cm,AD=5cm,那么BC等于( )
如图,△ABC≌△BAD,A和B,C和D是对应顶点,如果AB=6cm,BD=4cm,AD=5cm,那么BC等于( )| A. | 6cm | B. | 5cm | C. | 4cm | D. | 5cm或4cm |
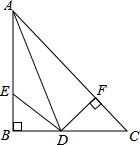 如图,AD为∠BAC的平分线,DF⊥AC于F,∠B=90°,DE=DC,试说明:BE=CF.
如图,AD为∠BAC的平分线,DF⊥AC于F,∠B=90°,DE=DC,试说明:BE=CF. 如图,直线AB、CD相交于点O,∠AOC=70°,OE把∠BOD分成两个角.且∠BOE:∠EOD=2:3,求∠EOD的度数.
如图,直线AB、CD相交于点O,∠AOC=70°,OE把∠BOD分成两个角.且∠BOE:∠EOD=2:3,求∠EOD的度数.