题目内容
7.若|x+1|与|2y+3|互为相反数,则x-y=$\frac{1}{2}$.分析 根据相反数的性质列出算式,根据非负数的性质求出x、y的值,把x、y的值代入所求的代数式计算即可.
解答 解:由相反数的性质可知,
|x+1|+|2y+3|=0,
即x+1=0,2y+3=0,
解得x=-1,y=-$\frac{3}{2}$,
x-y=-1+$\frac{3}{2}$=$\frac{1}{2}$,
故答案为:$\frac{1}{2}$.
点评 本题考查的是非负数的性质和相反数的性质,掌握相反数之和为0和非负数的性质是解题的关键.

练习册系列答案
相关题目
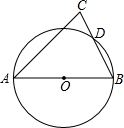 如图所示,AB是直径,D是圆上任意一点,D不与A,B重合,连接BD,并延长到点C,使DC=DB,连接AC,求证:AC=AB.
如图所示,AB是直径,D是圆上任意一点,D不与A,B重合,连接BD,并延长到点C,使DC=DB,连接AC,求证:AC=AB.