题目内容
16.用公式法解下列方程:(1)x2-10x+21=0;
(2)x2-3x-1=0;
(3)x2-7x+11=0;
(4)-5x2=2x-1.
分析 (1)(2)(3)找出a,b,c的值,代入求根公式计算即可;
(4)化为一般形式,找出a,b,c的值,代入求根公式计算即可.
解答 解:(1)∵a=1,b=-10,c=21,
∴b2-4ac=(-10)2-4×1×21=16,
∴x=$\frac{10±4}{2}$,
∴x1=7,x2=3.
(2)∵a=1,b=-3,c=-1,
∴b2-4ac=(-3)2-4×1×(-1)=13,
∴x=$\frac{3±\sqrt{13}}{2}$,
∴x1=$\frac{3+\sqrt{13}}{2}$,x2=$\frac{3-\sqrt{13}}{2}$.
(3)∵a=1,b=-7,c=11,
∴b2-4ac=(-7)2-4×1×11=5,
∴x=$\frac{7±\sqrt{5}}{2}$,
∴x1=$\frac{7+\sqrt{5}}{2}$,x2=$\frac{7-\sqrt{5}}{2}$.
(4)整理得5x2+2x-1=0
∵a=5,b=2,c=-1,
∴b2-4ac=22-4×5×(-1)=24,
∴x=$\frac{-2±2\sqrt{6}}{10}$,
∴x1=$\frac{-1+\sqrt{6}}{5}$,x2=$\frac{-1-\sqrt{6}}{5}$.
点评 本题考查了用公式法解一元二次方程,一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)的求根公式:x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$(b2-4ac≥0).

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
12.计算(2-5)+(-1)的结果是( )
| A. | 2 | B. | -2 | C. | 4 | D. | -4 |
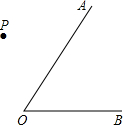 如图,已知点P是∠AOB的外部一点.
如图,已知点P是∠AOB的外部一点.