Question

13．如图，半圆O的直径AB=2，弦CD∥AB，∠COD=90°，则图中阴影部分的面积为$\frac{π}{4}$．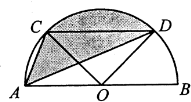

Answer 1

分析 由CD∥AB可知，点A、O到直线CD的距离相等，结合同底等高的三角形面积相等即可得出S_△ACD=S_△OCD，进而得出S_阴影=S_扇形COD，根据扇形的面积公式即可得出结论．

解答 解：∵弦CD∥AB，
∴S_△ACD=S_△OCD，
∴S_阴影=S_扇形COD=$\frac{∠COD}{360°}$•π•$（\frac{AB}{2}）^{2}$=$\frac{90°}{360°}$×π×$（\frac{2}{2}）^{2}$=$\frac{π}{4}$．
故答案为：$\frac{π}{4}$．

点评 本题考查了扇形面积的计算以及平行线的性质，解题的关键是找出S_阴影=S_扇形COD．本题属于基础题，难度不大，解决该题型题目时，通过分割图形找出面积之间的关系是关键．