题目内容
20.方程ax2+bx+c=0(a≠0)有两个相等的实数根,则有b2-4ac=0;若有两个不相等的实数根,则有b2-4ac>0;若方程无解,则有b2-4ac<0.分析 根据判别式的意义求解.
解答 解:方程ax2+bx+c=0(a≠0)有两个相等的实数根,则有b2-4ac=0;
若有两个不相等的实数根,则有b2-4ac>0;
若方程无解,则有b2-4ac<0.
故答案为b2-4ac=0;b2-4ac>0;b2-4ac<0.
点评 本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.

练习册系列答案
相关题目
9.下列条件中,能确定圆的是( )
| A. | 以点O为圆心 | B. | 以2cm长为半径 | ||
| C. | 以点O为圆心,以5cm长为半径 | D. | 经过已知点A |
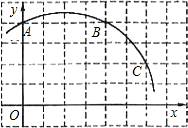 如图,直角坐标系中一条圆弧经过正方形网格的格点A(0,4)、B(4,4)、C(6,2).
如图,直角坐标系中一条圆弧经过正方形网格的格点A(0,4)、B(4,4)、C(6,2). 如图所示,△ABC∽△ACD,且AD=5,BD=4,求△ACD与△ABC的相似比.
如图所示,△ABC∽△ACD,且AD=5,BD=4,求△ACD与△ABC的相似比.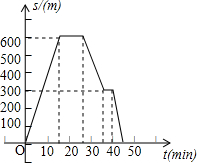 张爷爷晚饭以后外出散步,碰到老邻居,交谈了一会儿,返回途中在读报栏前看了一会儿报,如图是据此情境画出的图象,请你回答下面的问题:
张爷爷晚饭以后外出散步,碰到老邻居,交谈了一会儿,返回途中在读报栏前看了一会儿报,如图是据此情境画出的图象,请你回答下面的问题: