题目内容
8.若|x+2|+(y+3)2+$\sqrt{|x+y|+z}$=0,则x-y+z=-4.分析 直接利用绝对值以及偶次方和算术平方根的性质化简求出即可.
解答 解:∵|x+2|+(y+3)2+$\sqrt{|x+y|+z}$=0,
∴x+2=0,y+3=0,|x+y|+z=0,
解得:x=-2,y=-3,
∴|-2-3|+z=0,
解得:z=-5,
∴x-y+z=-2-(-3)-5=-4.
故答案为:-4.
点评 此题主要考查了绝对值以及偶次方和算术平方根,正确把握相关定义是解题关键.

练习册系列答案
相关题目
3.方程(x-2)(x+2)=x-2的解是( )
| A. | x=0 | B. | x=-1 | C. | x=2或x=-1 | D. | x=2或x=0 |
20.一元二次方程x2-(x+5)=2(3x-2)的一般形式是( )
| A. | x2-x-5=6x-4 | B. | x2-7x=1 | C. | x2-7x-1=0 | D. | x2-7x-9=0 |
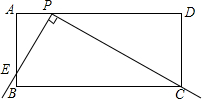 如图,在矩形ABCD中,AB=4,AD=10.直角尺的直角顶点P在AD上滑动时(点P与A、D不重合),一直角边经过点C,另一直角边AB交于点E.
如图,在矩形ABCD中,AB=4,AD=10.直角尺的直角顶点P在AD上滑动时(点P与A、D不重合),一直角边经过点C,另一直角边AB交于点E. 如图所示,已知AE⊥AB,△ACE≌△AFB,CE、AB、BF分别交于点D、M.证明:CE⊥BF.
如图所示,已知AE⊥AB,△ACE≌△AFB,CE、AB、BF分别交于点D、M.证明:CE⊥BF.