题目内容
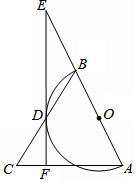
9.如图1,在正方形ABCD中,以BC为直径的正方形内,作半圆O,AE切半圆于点F交CD于点E,连接OA、OE.(1)求证:AO⊥EO;
(2)如图2,连接DF并延长交BC于点M,求$\frac{DF}{FM}$的值.
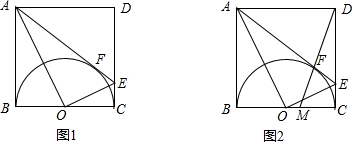
分析 (1)先证明AB和CD为⊙O的切线,则利用切线长定理得到OA平分∠BAE,OE平分∠AEC,从而得到∠AOE=90°,所以OA⊥OE;
(2)作FH⊥CD于H,如图,设正方形ABCD的边长为4a,AF=AB=4a,OB=OC=2a,先证明Rt△ABO∽Rt△OCE,利用相似比得到CE=a,则EA=5a,ED=3a,再证明△EFH∽△EAD,利用相似比求出FH=$\frac{5}{4}$a,EH=$\frac{3}{4}$a,则DH=$\frac{9}{4}$a,然后根据平行线分线段成比例定理即可得到结论.
解答 (1)证明:∵四边形ABCD为正方形,
∴∠B=∠C=90°,AB∥CD,
∴AB和CD为⊙O的切线,
∵AE切半圆于点F,
∴OA平分∠BAE,OE平分∠AEC,
而AB∥CD,
∴∠BAE+∠AEC=180°,
∴∠OAE+∠OEA=90°,
∴∠AOE=90°,
∴OA⊥OE;
(2)解:作FH⊥CD于H,如图,设正方形ABCD的边长为4a,
则AF=AB=4a,OB=OC=2a,
∵∠AOE=90°,
∴∠AOB+∠COE=90°,
∵∠AOB+∠OAB=90°,
∴∠OAB=∠EOC,
∴Rt△ABO∽Rt△OCE,
∴AB:OC=OB:CE,即4a:2a=2a:CE,解得CE=a,
∴EF=EC=a,
∴EA=5a,ED=3a,
∵FH∥AD,
∴△EFH∽△EAD,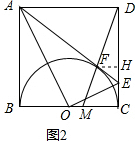
∴$\frac{FH}{AD}$=$\frac{EF}{EA}$=$\frac{EH}{ED}$,即$\frac{FH}{5a}$=$\frac{a}{4a}$=$\frac{EH}{3a}$,
∴FH=$\frac{5}{4}$a,EH=$\frac{3}{4}$a,
∴DH=3a-$\frac{3}{4}$a=$\frac{9}{4}$a,
∴CH=4a-$\frac{9}{4}$a=$\frac{7}{4}$a,
∵FH∥CM,
∴$\frac{DF}{FM}$=$\frac{DH}{CH}$=$\frac{9}{7}$.
点评 本题考查了相似三角形的判定和性质,切线的性质,正方形的性质和解直角三角形,正确的作出辅助线是解题的关键.

| A. | 0 | B. | 1 | C. | -$\frac{1}{2}$ | D. | -π |
| A. | (1-20%)(1+x)2=1+15% | B. | (1+15%%)(1+x)2=1-20% | ||
| C. | 2(1-20%)(1+x)=1+15% | D. | 2(1+15%)(1+x)=1-20% |
| A. | 2 | B. | $\sqrt{2}$ | C. | 4 | D. | ±2 |
| A. | -$\sqrt{2}$ | B. | -1 | C. | 0 | D. | 1 |
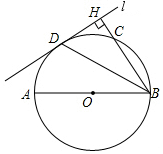 如图,AB为⊙O的直径,直线1切⊙O于点D,过点B作BH⊥1于点H,交⊙O于点C,连接BD.
如图,AB为⊙O的直径,直线1切⊙O于点D,过点B作BH⊥1于点H,交⊙O于点C,连接BD.
 如图,在△ABC中,AB=AC,以AB为直径的半圆交BC于点D,过点D作EF⊥AC于点F,交AB的延长线于点E.
如图,在△ABC中,AB=AC,以AB为直径的半圆交BC于点D,过点D作EF⊥AC于点F,交AB的延长线于点E. 如图,直线MN交⊙O于A、B两点,AC是⊙O的直径,AD平分∠CAM交⊙O于D,过点D作⊙O的切线交MN于点E.
如图,直线MN交⊙O于A、B两点,AC是⊙O的直径,AD平分∠CAM交⊙O于D,过点D作⊙O的切线交MN于点E.