题目内容
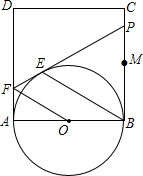 如图,正方形ABCD的边长为2,点M是BC的中点,P是线段MC上的一个动点(不与M、C重合),以AB为直径作⊙O,过点P作⊙O的切线,交AD于点F,切点为E.
如图,正方形ABCD的边长为2,点M是BC的中点,P是线段MC上的一个动点(不与M、C重合),以AB为直径作⊙O,过点P作⊙O的切线,交AD于点F,切点为E.(1)求证:OF∥BE;
(2)设BP=x,AF=y,求y关于x的函数解析式,并写出自变量x的取值范围.
考点:切线的性质,全等三角形的判定与性质,正方形的性质
专题:
分析:(1)连接OE,根据切线的性质求得OA⊥FA,OE⊥EF,FA=FE,根据角的平分线定理的逆定理求得∴∠AOF=∠EOF=
∠AOE,然后求得∠OBE=∠OEB,∠AOE=∠OBE+∠OEB=2∠OBE,从而求得∠AOF=∠OBE,根据平行线的判定证得OF∥BE;
(2)过F作FQ⊥BC于Q,根据勾股定理即可求得y关于x的函数解析式.
| 1 |
| 2 |
(2)过F作FQ⊥BC于Q,根据勾股定理即可求得y关于x的函数解析式.
解答: (1)证明:连接OE,
(1)证明:连接OE,
∵FE、FA是⊙O的两条切线,
∴OA⊥FA,OE⊥EF,FA=FE,
∴∠AOF=∠EOF=
∠AOE,
又∵OB=OE,
∴∠OBE=∠OEB,∠AOE=∠OBE+∠OEB=2∠OBE
∴∠AOF=∠OBE.
∴OF∥BE;
(2)解:过F作FQ⊥BC于Q,
∴PQ=BP-BQ=x-y,PF=EF+EP=FA+BP=x+y,
∵在Rt△PFQ中,FQ2+QP2=PF2,
∴22+(x-y)2=(x+y)2,
化简得y=
,(1<x<2).
 (1)证明:连接OE,
(1)证明:连接OE,∵FE、FA是⊙O的两条切线,
∴OA⊥FA,OE⊥EF,FA=FE,
∴∠AOF=∠EOF=
| 1 |
| 2 |
又∵OB=OE,
∴∠OBE=∠OEB,∠AOE=∠OBE+∠OEB=2∠OBE
∴∠AOF=∠OBE.
∴OF∥BE;
(2)解:过F作FQ⊥BC于Q,
∴PQ=BP-BQ=x-y,PF=EF+EP=FA+BP=x+y,
∵在Rt△PFQ中,FQ2+QP2=PF2,
∴22+(x-y)2=(x+y)2,
化简得y=
| 1 |
| x |
点评:本题考查了切线的性质,正方形的性质,角平分线的性质定理的逆定理,勾股定理的应用等;作出辅助线构建等腰三角形和矩形是本题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
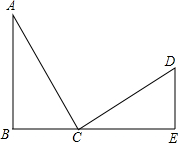 如图,∠B=∠E=90°,AB=CE,AC=CD,∠D=60°,CD=8cm.求:
如图,∠B=∠E=90°,AB=CE,AC=CD,∠D=60°,CD=8cm.求: