题目内容
已知△ABC中,BC=
+1,∠B=45°,∠C=30°,求△ABC的面积.
| 3 |
考点:解直角三角形
专题:计算题
分析:作AD⊥BC于D,如图,设BD=x,在Rt△ABD中,由于∠B=45°,可判断△ABD为等腰直角三角形,则AD=x,在Rt△ACD中,根据含30°的直角三角形三边的关系得到CD=
AD=
x,所以x+
x=
+1,解得x=1,则AD=1,然后根据三角形面积公式求解.
| 3 |
| 3 |
| 3 |
| 3 |
解答:解:作AD⊥BC于D,如图,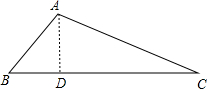 设BD=x,
设BD=x,
在Rt△ABD中,∵∠B=45°,
∴△ABD为等腰直角三角形,
∴AD=BD=x,
在Rt△ACD中,∵∠C=30°,
∴CD=
AD=
x,
而BD+CD=BC,
∴x+
x=
+1,解得x=1,
∴AD=1,
∴△ABC的面积=
•AD•BC=
•1•(
+1)=
.
 设BD=x,
设BD=x,在Rt△ABD中,∵∠B=45°,
∴△ABD为等腰直角三角形,
∴AD=BD=x,
在Rt△ACD中,∵∠C=30°,
∴CD=
| 3 |
| 3 |
而BD+CD=BC,
∴x+
| 3 |
| 3 |
∴AD=1,
∴△ABC的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
点评:本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.

练习册系列答案
相关题目
苹果的单价为a元/千克,香蕉的单价为b元/千克,买3千克苹果和2千克香蕉共需( )
| A、(a+b)元 |
| B、(3a+2b)元 |
| C、(2a+3b)元 |
| D、5(a+b)元 |
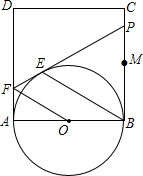 如图,正方形ABCD的边长为2,点M是BC的中点,P是线段MC上的一个动点(不与M、C重合),以AB为直径作⊙O,过点P作⊙O的切线,交AD于点F,切点为E.
如图,正方形ABCD的边长为2,点M是BC的中点,P是线段MC上的一个动点(不与M、C重合),以AB为直径作⊙O,过点P作⊙O的切线,交AD于点F,切点为E. 如图,BE⊥CD,DF⊥BC,BE=DE,BC=10,CE=6,求AB的长.
如图,BE⊥CD,DF⊥BC,BE=DE,BC=10,CE=6,求AB的长. 在四边形ABCO中,∠AOC=∠OCB=90°,AO=2,OC=8,CB=8
在四边形ABCO中,∠AOC=∠OCB=90°,AO=2,OC=8,CB=8 如图,Rt△BC中,∠BAC=90°,AD⊥BC于D,E是AC上任意一点,连接BE,过A作AF⊥BE于F,求证:BD•BC=BF•BE.
如图,Rt△BC中,∠BAC=90°,AD⊥BC于D,E是AC上任意一点,连接BE,过A作AF⊥BE于F,求证:BD•BC=BF•BE.