题目内容
已知方程x2-(2m-1)x-4m+2=0的两个实数根的平方和等于5,则m= .
考点:根与系数的关系,根的判别式
专题:计算题
分析:设方程的两实数根为a、b,根据根与系数的关系得到a+b=2m-1,ab=-4m+2,再把a2+b2=5变形得(a+b)2-2ab=5,则(2m-1)2-2(-4m+2)=5,
解得m1=-2,m2=1,然后根据根得判别式确定满足条件的m的值.
解得m1=-2,m2=1,然后根据根得判别式确定满足条件的m的值.
解答:解:设方程的两实数根为a、b,
根据题意得a+b=2m-1,ab=-4m+2,
∵a2+b2=5,
∴(a+b)2-2ab=5,
∴(2m-1)2-2(-4m+2)=5,
整理得m2+m-2=0,解得m1=-2,m2=1,
当m=-2时,方程变形为x2+5x+10,△<0,方程没有实数解,
∴m的值为1.
故答案为1.
根据题意得a+b=2m-1,ab=-4m+2,
∵a2+b2=5,
∴(a+b)2-2ab=5,
∴(2m-1)2-2(-4m+2)=5,
整理得m2+m-2=0,解得m1=-2,m2=1,
当m=-2时,方程变形为x2+5x+10,△<0,方程没有实数解,
∴m的值为1.
故答案为1.
点评:本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
.也考查了根的判别式.
| b |
| a |
| c |
| a |

练习册系列答案
相关题目
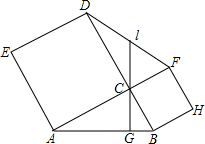 在△ABC中,∠ACB=90°,以AB、BC为边向△ABC外分别作正方形CBHF和正方形ACDE,连接DF,过点C作CG⊥AB,垂足为G,且CG的反向延长线与DF交于点I.
在△ABC中,∠ACB=90°,以AB、BC为边向△ABC外分别作正方形CBHF和正方形ACDE,连接DF,过点C作CG⊥AB,垂足为G,且CG的反向延长线与DF交于点I.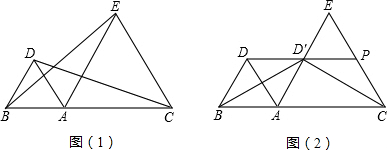
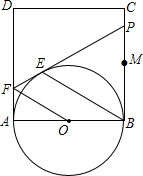 如图,正方形ABCD的边长为2,点M是BC的中点,P是线段MC上的一个动点(不与M、C重合),以AB为直径作⊙O,过点P作⊙O的切线,交AD于点F,切点为E.
如图,正方形ABCD的边长为2,点M是BC的中点,P是线段MC上的一个动点(不与M、C重合),以AB为直径作⊙O,过点P作⊙O的切线,交AD于点F,切点为E. 如图,BM、CM平分△ABC的外角∠CBE和∠BCF,且BM与CM交于点M,ME⊥BE于E,MF⊥CF于点F.求证:ME=MF.
如图,BM、CM平分△ABC的外角∠CBE和∠BCF,且BM与CM交于点M,ME⊥BE于E,MF⊥CF于点F.求证:ME=MF.