Question

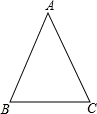
在等边△ABC中，AB=2cm，点D是BC边上的任意一点，DE⊥AB于点E，DF⊥AC于点F，BN⊥AC于点N，则DE+DF=__________ cm．

Answer 1

 cm．

【考点】等边三角形的性质．

【分析】作AG⊥BC于G，根据等边三角形的性质得出∠B=60°，解直角三角形求得AG=，根据S_△ABD+S_△ACD=S_△ABC即可得出DE+DF=AG=cm．

【解答】解：作AG⊥BC于G，

∵△ABC是等边三角形，

∴∠B=60°，

∴AG=AB=cm，

连接AD，

∵S_△ABD+S_△ACD=S_△ABC，

∴AB•DE+AC•DF=BC•AG，

∵AB=AC=BC=2，

∴DE+DF=AG=cm，

故答案为．

【点评】本题考查了等边三角形的性质，解直角三角函数以及三角形面积等，根据S_△ABD+S_△ACD=S_△ABC即可得出DE+DF=AG是解题的关键．