题目内容
4.在数学活动中,小明遇到了求式子$\frac{1}{2}+$$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+…+$\frac{1}{{2}^{n}}$的值(结果用n表示),他和同伴讨论设计了如图①所示的几何图形,想利用图形来求式子的值.(1)利用图①,求$\frac{1}{2}+$$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$$+\frac{1}{{2}^{4}}$的值;
(2)经过思考,小明将图形①变成图形②,能求$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+…+$\frac{1}{{2}^{n}}$的值吗?
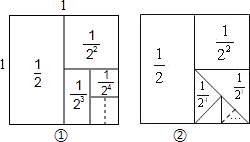
分析 (1)用总面积减去剩下的面积即可得出答案;
(2)因为每一次分割都是前面图形的$\frac{1}{2}$,可以用总面积减去剩下的面积求得答案即可.
解答 解:(1)$\frac{1}{2}+$$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$$+\frac{1}{{2}^{4}}$
=1-$\frac{1}{{2}^{4}}$;
(2)能.
$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+…+$\frac{1}{{2}^{n}}$
=1-$\frac{1}{{2}^{n}}$.
点评 此题考查图形的变化规律,找出图形之间的联系,得出运算规律,利用规律,解决问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.如何平移抛物线y=-2x2-1得到抛物线y=-2x2+4x-1呢?( )
| A. | 向右平移4个单位 | |
| B. | 先向左平移1个单位,再向上平移2个单位 | |
| C. | 向左平移4个单位 | |
| D. | 先向右平移1个单位,再向上平移2个单位 |
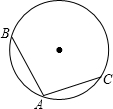 如图.⊙O的半径为2$\sqrt{2}$,AB、AC是⊙O的两条弦,AB=2$\sqrt{3}$,AC=4,如果以O为圆心,作一个与直线AC相切的圆,那么:
如图.⊙O的半径为2$\sqrt{2}$,AB、AC是⊙O的两条弦,AB=2$\sqrt{3}$,AC=4,如果以O为圆心,作一个与直线AC相切的圆,那么: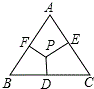 如图所示,在△ABC中,∠A=∠B=∠C,P是三角形内任意一点,PD⊥BC于D,PE⊥AC于E,PF⊥AB于F,AB=a,试说明PD+PE+PF为定值.
如图所示,在△ABC中,∠A=∠B=∠C,P是三角形内任意一点,PD⊥BC于D,PE⊥AC于E,PF⊥AB于F,AB=a,试说明PD+PE+PF为定值.