题目内容
19.如图①,一条笔直的公路上有A、B、C 三地,B、C 两地相距 150 千米,甲、乙两辆汽车分别从B、C 两地同时出发,沿公路匀速相向而行,分别驶往C、B 两地.甲、乙两车到A 地的距离y1、y2(千米)与行驶时间 x(时)的关系如图②所示.
根据图象进行以下探究:
(1)请在图①中标出A地的位置,并作简要的文字说明;
(2)求图②中M点的坐标,并解释该点的实际意义;
(3)在图②中补全甲车到达C地的函数图象,并求甲车到 A地的距离y1与行驶时间x的函数关系式;
(4)A地设有指挥中心,指挥中心及两车都配有对讲机,两部对讲机在15千米之内(含15千米)时能够互相通话,求两车可以同时与指挥中心用对讲机通话的时间.
分析 (1)由图②得:AB=60km或者AC=90km,则AB:AC=2:3,据此画图;
(2)由图②得:乙车从C地到B地一共需要2小时,则速度=150÷2=75km/h,又知C地到A地路程为90km,所以时间为:90÷75=1.2,得出M的坐标;并表示M点是乙车到达A地;
(3)根据(1,0)、(0,60)求y1与行驶时间x的函数关系式;计算甲的速度为60km/h,最后计算甲走完全程的时间为:150÷60=2.5,根据(1,0)、(2.5,90)画线段;
(4)分别求DM、MC、BC的解析式,求两车距离A地小于等于15km时对应的时间,并计算时间差即可.
解答  解:(1)如图①,满足AB:AC=2:3,
解:(1)如图①,满足AB:AC=2:3,
即AB=60km或者AC=90km;
(2)150÷2=75,
∴t=90÷75=1.2时,
∴M(1.2,0),表示此时乙车到达A地,
(3)当0<x<1.2时,设AB的解析式为:y1=kx+b,
把(1,0)、(0,60)代入得:$\left\{\begin{array}{l}{k+b=0}\\{b=60}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-60}\\{b=60}\end{array}\right.$,
∴y1=-60x+60,
甲的速度为:60÷1=60,
∴150÷60=2.5,
如图②所示,补充甲甲车到达C地的函数图象;
(4)同理BC的解析式为:y1=60x-60,
DM的解析式为:y2=-75x+90,
ME的解析式为:y2=75x-90,
由题意得:$\left\{\begin{array}{l}{-60x+60≤15}\\{60x-60≤15}\end{array}\right.$,
解得:$\frac{3}{4}$≤x≤$\frac{5}{4}$,
由题意得:$\left\{\begin{array}{l}{-75x+90≤15}\\{75x-90≤15}\end{array}\right.$,
解得:1≤x≤$\frac{7}{5}$,
∴1≤x≤$\frac{5}{4}$,
$\frac{5}{4}$-1=$\frac{1}{4}$,
∴两车可以同时与指挥中心用对讲机通话的时间$\frac{1}{4}$小时=15分钟.
点评 本题是一次函数的应用,属于行程问题,利用平面直角坐标系读出已知条件,有难度,关键是读懂题意,结合图象确定点的坐标,根据点的坐标求一次函数解析式;再根据解析式解决问题.

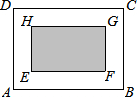 在一块长12m,宽8m的长方形平地中央,划出地方砌一个面积为32m2的长方形花台,要使花坛四周的宽地宽度一样,则这个宽度为多少?
在一块长12m,宽8m的长方形平地中央,划出地方砌一个面积为32m2的长方形花台,要使花坛四周的宽地宽度一样,则这个宽度为多少?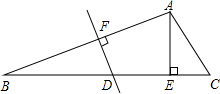 如图,△ABC中,∠C=60°,AB的垂直平分线交BC于点D,DE=6,BD=6$\sqrt{2}$,AE⊥BC于E,求EC的长.
如图,△ABC中,∠C=60°,AB的垂直平分线交BC于点D,DE=6,BD=6$\sqrt{2}$,AE⊥BC于E,求EC的长. 如图,点D在△ABC的AB边上,且DC=DA.
如图,点D在△ABC的AB边上,且DC=DA.