题目内容
2.(1)填空:31-30=2×3( ),
32-31=2×3( ),
33-32=2×3( ),
…
(2)探索(1)中式子的规律,试写出第n个等式,并说明第n个等式成立;
(3)计算30+31+32+…+32016.
分析 (1)根据有理数的乘方的定义进行计算即可得解;
(2)根据指数结果幂的指数比等式的序数小1解答;
(3)设S=3°+31+32+33+…+32015+32016,然后表示出3S,再相减计算即可得解.
解答 解:(1)31-30=2×30,32-31=2×31,33-32=2×32.
故答案为:0,1,2;
(2)规律:3n-3n-1=2×3n-1,
证明:3n-3n-1=3×3n-1-1×3n-1=2×3n-1;
(3)设S=3°+31+32+33+…+32015+32016,
则3S=31+32+33+…+32015+32017,
所以2S=(31+32+33+…+32015+32017)-(30+31+32+33+…+32015+32016)=32017-1,
S=$\frac{1}{2}$(32017-1).
点评 本题主要考查了数字变化规律,利用有理数的乘方的计算,利用整体思想求解是解答此题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
15.在代数式:$\frac{ab}{3}$,-$\frac{2}{3}$abc,0,-5a,x-y,$\frac{2}{x}$,$\frac{1}{π}$中,单项式有( )
| A. | 6个 | B. | 5个 | C. | 4个 | D. | 3个 |
13.计算:(-3)+5的结果是( )
| A. | -2 | B. | 2 | C. | 8 | D. | -8 |
7.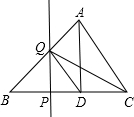 如图,△ABC中,AD⊥BC,垂足为D,AD=BD=3,CD=2,点P从点B出发沿线段BC的方向移动到点C停止,过点P作PQ⊥BC,交折线BA-AC于点Q,连接DQ、CQ,若△ADQ与△CDQ的面积相等,则线段BP的长度是( )
如图,△ABC中,AD⊥BC,垂足为D,AD=BD=3,CD=2,点P从点B出发沿线段BC的方向移动到点C停止,过点P作PQ⊥BC,交折线BA-AC于点Q,连接DQ、CQ,若△ADQ与△CDQ的面积相等,则线段BP的长度是( )
 如图,△ABC中,AD⊥BC,垂足为D,AD=BD=3,CD=2,点P从点B出发沿线段BC的方向移动到点C停止,过点P作PQ⊥BC,交折线BA-AC于点Q,连接DQ、CQ,若△ADQ与△CDQ的面积相等,则线段BP的长度是( )
如图,△ABC中,AD⊥BC,垂足为D,AD=BD=3,CD=2,点P从点B出发沿线段BC的方向移动到点C停止,过点P作PQ⊥BC,交折线BA-AC于点Q,连接DQ、CQ,若△ADQ与△CDQ的面积相等,则线段BP的长度是( )| A. | $\frac{9}{5}$或4 | B. | $\frac{6}{5}$或4 | C. | $\frac{9}{5}$或$\frac{13}{5}$ | D. | $\frac{6}{5}$或$\frac{13}{5}$ |
12.下列方程中是关于x的一元二次方程的是( )
| A. | x2+$\frac{1}{{x}^{2}}$=1 | B. | (x-1)(x+2)=1 | C. | ax2+bx+c=0 | D. | 3x2-5xy-5y2=0 |
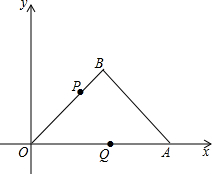 如图,∠OAB=45°,点A的坐标是(4,0),AB=$2\sqrt{2}$,连结OB.
如图,∠OAB=45°,点A的坐标是(4,0),AB=$2\sqrt{2}$,连结OB.