题目内容
15.函数y=kx-1(k≠0)的图象向上平移一个单位后与反比例函数y=$\frac{4}{x}$的图象的交点为A、B,若A点坐标为(-1,-4),则B点的坐标为(1,4).分析 根据平移的性质找出平移后的一次函数的解析式,再根据平移后的一次函数与反比例函数图象均关于原点对称,由此即可得出点A、B关于原点对称,根据点A的坐标求出点B的坐标,此题得解.
解答 解:函数y=kx-1(k≠0)的图象向上平移一个单位后得到的函数为y=kx-1+1=kx(k≠0),
∵函数y=kx(k≠0)的图象关于原点对称,反比例函数y=$\frac{4}{x}$的图象关于原点对称,
∴两函数图象的交点A、B关于原点对称,
∵点A的坐标为(-1,-4),
∴点B的坐标为(1,4).
故答案为:(1,4).
点评 本题考查了反比例函数与一次函数的交点问题已经平移的性质,解题的关键是得出点A、B关于原点对称.本题属于基础题,难度不大,解决该题型题目时,利用平移的性质找出一次函数平移后的解析式,结合两函数的对称性得出点A、B关于原点对称是关键.

练习册系列答案
相关题目
5.若三角形的两条边长分别为6cm和10cm,则它的第三边长不可能为( )
| A. | 5cm | B. | 8cm | C. | 10cm | D. | 17cm |
3. 如图,某小区规划在一个长AD=40m,宽AB=26m的矩形场地ABCD上修建三条同样宽的通道(图中阴影部分),使其中两条与AB平行,另一条与AD平行,其余部分种植花草,要使每一块种植花草的场地面积都是144m2.若设通道的宽度为x(m),则根据题意所列的方程是( )
如图,某小区规划在一个长AD=40m,宽AB=26m的矩形场地ABCD上修建三条同样宽的通道(图中阴影部分),使其中两条与AB平行,另一条与AD平行,其余部分种植花草,要使每一块种植花草的场地面积都是144m2.若设通道的宽度为x(m),则根据题意所列的方程是( )
 如图,某小区规划在一个长AD=40m,宽AB=26m的矩形场地ABCD上修建三条同样宽的通道(图中阴影部分),使其中两条与AB平行,另一条与AD平行,其余部分种植花草,要使每一块种植花草的场地面积都是144m2.若设通道的宽度为x(m),则根据题意所列的方程是( )
如图,某小区规划在一个长AD=40m,宽AB=26m的矩形场地ABCD上修建三条同样宽的通道(图中阴影部分),使其中两条与AB平行,另一条与AD平行,其余部分种植花草,要使每一块种植花草的场地面积都是144m2.若设通道的宽度为x(m),则根据题意所列的方程是( )| A. | (40-x)(26-2x)=144×6 | B. | (40-2x)(26-x)=144×6 | C. | (40-2x)(26-x)=144÷6 | D. | (40-x)(26-2x)=144÷6 |
10.在下面四个几何体中,主视图与俯视图都是圆的为( )
| A. | 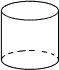 | B. | 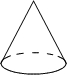 | C. | 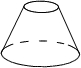 | D. | 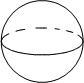 |
20.下面调查统计中,适合做全面调查的是( )
| A. | 乘坐飞机的旅客是否携带了违禁物品 | |
| B. | 苹果电脑的市场占有率 | |
| C. | “我爱发明”专栏电视节目的收视率 | |
| D. | “现代”汽车每百公里的耗油量 |
5. 已知M、N、P、Q四点的位置如图所示,下列结论中,正确的是( )
已知M、N、P、Q四点的位置如图所示,下列结论中,正确的是( )
 已知M、N、P、Q四点的位置如图所示,下列结论中,正确的是( )
已知M、N、P、Q四点的位置如图所示,下列结论中,正确的是( )| A. | ∠NOQ=42° | B. | ∠NOP=132° | C. | ∠PON比∠MOQ大 | D. | ∠MOQ与∠MOP互补 |

 如图,在矩形ABCD中,点A为坐标原点,点B在x轴正半轴,点D在y轴正半轴,点C坐标为(6,m),点E是CD的中点,以CE为一边在矩形ABCD的内部作矩形CEFG,使点F在直线y=x上,交线段BC于点G,直线DG的函数表达式为y=-$\frac{1}{6}$x+4,直线DG和AF交于点H.
如图,在矩形ABCD中,点A为坐标原点,点B在x轴正半轴,点D在y轴正半轴,点C坐标为(6,m),点E是CD的中点,以CE为一边在矩形ABCD的内部作矩形CEFG,使点F在直线y=x上,交线段BC于点G,直线DG的函数表达式为y=-$\frac{1}{6}$x+4,直线DG和AF交于点H.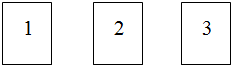 如图,三张卡片形状、大小、质地相同,分别印数字1、2、3,现将它们放入盒子.若从盒子中任取一张卡片,求取到数字是奇数的卡片的概率是$\frac{2}{3}$.
如图,三张卡片形状、大小、质地相同,分别印数字1、2、3,现将它们放入盒子.若从盒子中任取一张卡片,求取到数字是奇数的卡片的概率是$\frac{2}{3}$.