题目内容
1．计算：$\frac{1}{x}$-$\frac{2}{3x}$+$\frac{x}{3x-2}$．分析 原式通分并利用同分母分式的加减法则计算即可得到结果．
解答 解：原式=$\frac{3（3x-2）}{3x（3x-2）}$-$\frac{2（3x-2）}{3x（3x-2）}$+$\frac{3{x}^{2}}{3x（3x-2）}$
=$\frac{9x-6-6x+4+3{x}^{2}}{9{x}^{2}-6x}$
=$\frac{3{x}^{2}+3x-2}{9{x}^{2}-6x}$．
点评 此题考查了分式的加减法，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
9．
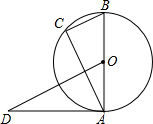如图，AB是⊙O的直径，AD是⊙O的切线，点C在⊙O上，BC∥OD，AB=2，OD=3，则BC的长为（ ）
如图，AB是⊙O的直径，AD是⊙O的切线，点C在⊙O上，BC∥OD，AB=2，OD=3，则BC的长为（ ）| A． | $\frac{2}{3}$ | B． | $\frac{3}{2}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | $\frac{\sqrt{2}}{2}$ |
如图，?ABCD和?EAFC的顶点为D，B，E，F在同一条直线上．求证：DE=BF．
如图，过?ABCD的各顶点分别作对角线的垂线AE、BF、CG、DH．垂足分别为E、F、G、H．求证：四边形EFGH是平行四边形．
已知如图，∠1=∠2，CF⊥AB、DE⊥AB，那么∠AFG和∠B是否相等，请说明理由．