题目内容
5.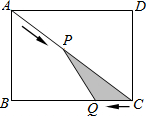 如图,在矩形ABCD中,AB=6cm,BC=8cm,动点P以2cm/s的速度从点A出发,沿AC向点C移动,同时动点Q以1cm/s的速度从点C出发,沿CB向点B移动,设P、Q两点移动ts(0<t<5)后,△CQP的面积为S cm2.在P、Q两点移动的过程中,△CQP的面积能否等于3.6cm2?若能,求出此时t的值;若不能,请说明理由.
如图,在矩形ABCD中,AB=6cm,BC=8cm,动点P以2cm/s的速度从点A出发,沿AC向点C移动,同时动点Q以1cm/s的速度从点C出发,沿CB向点B移动,设P、Q两点移动ts(0<t<5)后,△CQP的面积为S cm2.在P、Q两点移动的过程中,△CQP的面积能否等于3.6cm2?若能,求出此时t的值;若不能,请说明理由.
分析 在矩形ABCD中求出对角线AC的长度,然后表示出CQ、PC的长度,过点P作PH⊥BC于点H,然后在Rt△PHC中表示出PH的长度,根据面积为3.6cm2,列方程求解.
解答 解:在矩形ABCD中,
∵AB=6cm,BC=8cm,
∴AC=10cm,AP=2tcm,PC=(10-2t)cm,
CQ=tcm,
过点P作PH⊥BC于点H,
则PH=$\frac{3}{5}$(10-2t)cm,
根据题意,得 $\frac{1}{2}$t•$\frac{3}{5}$(10-2t)=3.6,
解得:t1=2,t2=3.
答:△CQP的面积等于3.6cm2时,t的值为2或3.
点评 本题考查了一元二次方程的应用,解答本题的关键是读懂题意,表示出CQ、PC的长度,求出三角形的面积,然后解方程.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
10. 在正方形上给定8个点,以这些点为顶点,能构成( )个等腰三角形.
在正方形上给定8个点,以这些点为顶点,能构成( )个等腰三角形.
 在正方形上给定8个点,以这些点为顶点,能构成( )个等腰三角形.
在正方形上给定8个点,以这些点为顶点,能构成( )个等腰三角形.| A. | 12 | B. | 16 | C. | 20 | D. | 24 |
15.多项式3x4-5x2y-2xy4-7是 次 项式( )
| A. | 4,3 | B. | 5,4 | C. | 5,5 | D. | 4,5 |
 如图所示,将一个矩形沿图中的虚线折叠,用量角器测量一下其中的α,β,得α=β
如图所示,将一个矩形沿图中的虚线折叠,用量角器测量一下其中的α,β,得α=β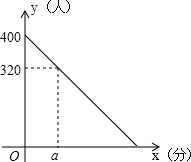 春节期间,某客运站旅客流量不断增大,旅客往往需长时间排队等候购票.经调查发现,每天开始售票时,约有400名旅客排队等候购票,同时又有新的旅客不断进入售票厅排队等候购票.售票时售票厅每分钟新增购票人数4人,每分钟每个售票窗口出售的票数3张,规定每人只购一张票.某天若同时开放两个售票窗口,售票厅排队等候购票的人数y(人)与售票时间x(分)的关系如图所示.
春节期间,某客运站旅客流量不断增大,旅客往往需长时间排队等候购票.经调查发现,每天开始售票时,约有400名旅客排队等候购票,同时又有新的旅客不断进入售票厅排队等候购票.售票时售票厅每分钟新增购票人数4人,每分钟每个售票窗口出售的票数3张,规定每人只购一张票.某天若同时开放两个售票窗口,售票厅排队等候购票的人数y(人)与售票时间x(分)的关系如图所示.