题目内容
17.A、B两地相距400km,甲、乙两车分别从A、B两地同时出发,相向而行,甲车以每小时100km的速度匀速行驶1h后,休息了1h,然后按原速继续行驶到B地,乙车以每小时80km的速度匀速行驶到A地.(1)当乙车经过甲车休息的地方时,乙车行驶的时间是$\frac{15}{4}$h;
(2)当甲、乙两车相遇时,求乙车行驶的时间;
(3)当甲、乙两车相距40km时,求乙车行驶的时间.
分析 (1)设乙车行驶的时间是xh,根据甲车以每小时100km的速度匀速行驶1h后,开始休息,列出方程求解即可;
(2)设乙车行驶了xh,甲、乙两车相遇,根据甲行驶的路程+乙行驶的路程=总路程,列方程求解即可;
(3)设乙车行驶的时间是yh,甲、乙两车相距40km,分两种情况讨论:相遇前和相遇后,根据甲行驶的路程+乙行驶的路程=总路程-40和甲行驶的路程+乙行驶的路程=总路程+40,列方程求解即可.
解答 解:(1)设乙车行驶的时间是xh,根据题意得:
80x=400-100×1,
解得:x=$\frac{15}{4}$.
答:当乙车经过甲车休息的地方时,乙车行驶的时间是$\frac{15}{4}$.
故答案为:$\frac{15}{4}$;
(2)设乙车行驶了xh,甲、乙两车相遇,根据题意得:
100(x-1)+80x=400,
解得:x=$\frac{25}{9}$.
答:乙车行驶了$\frac{25}{9}$h,甲、乙两车相遇;
(3)设乙车行驶的时间是yh,甲、乙两车相距40km,根据题意得:
①相遇前:100(y-1)+80y=400-40,
解得:y=$\frac{23}{9}$;
②相遇后:100(y-1)+80y=400+40,
解得:y=3.
答:乙车行驶的时间是$\frac{23}{9}$h或3h,甲、乙两车相距40km.
点评 此题考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.已知关于x的方程(k-3)x|k|-1+(2k-3)x+4=0是一元二次方程,则k的值应为( )
| A. | ±3 | B. | 3 | C. | -3 | D. | 不能确定 |
12.若关于x的方程3x+3a=2的解是正数,则a的取值范围是( )
| A. | a≤$\frac{2}{3}$ | B. | a≥$\frac{2}{3}$ | C. | a>$\frac{2}{3}$ | D. | a<$\frac{2}{3}$ |
2.下列计算中正确的是( )
| A. | 3a+2a=5a2 | B. | 2a2•a3=2a6 | C. | (2a+b)(2a-b)=2a2-b2 | D. | (2ab)2=4a2b2 |
7.如图是甲、乙两个商店一年内销售电视机数量的统计图.( )
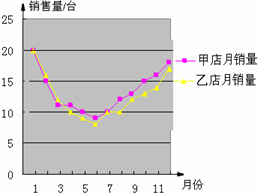

| A. | 12月份是这两个商店销售最高峰期 | B. | 第一季度总销售量乙店比甲店多 | ||
| C. | 上半年这两个商店销售逐月提高 | D. | 下半年这两个商店销售逐月减少 |
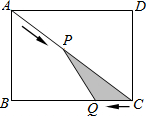 如图,在矩形ABCD中,AB=6cm,BC=8cm,动点P以2cm/s的速度从点A出发,沿AC向点C移动,同时动点Q以1cm/s的速度从点C出发,沿CB向点B移动,设P、Q两点移动ts(0<t<5)后,△CQP的面积为S cm2.在P、Q两点移动的过程中,△CQP的面积能否等于3.6cm2?若能,求出此时t的值;若不能,请说明理由.
如图,在矩形ABCD中,AB=6cm,BC=8cm,动点P以2cm/s的速度从点A出发,沿AC向点C移动,同时动点Q以1cm/s的速度从点C出发,沿CB向点B移动,设P、Q两点移动ts(0<t<5)后,△CQP的面积为S cm2.在P、Q两点移动的过程中,△CQP的面积能否等于3.6cm2?若能,求出此时t的值;若不能,请说明理由.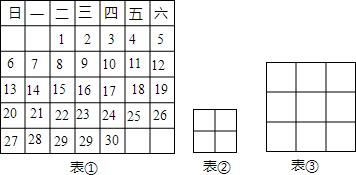
 如图,平面内有公共端点的六条射线OA,OB,OC,OD,OE,OF.从射线OA开始按逆时针方向依次在射线上写出数字1,2,3,4,5,6,7,….
如图,平面内有公共端点的六条射线OA,OB,OC,OD,OE,OF.从射线OA开始按逆时针方向依次在射线上写出数字1,2,3,4,5,6,7,….