题目内容
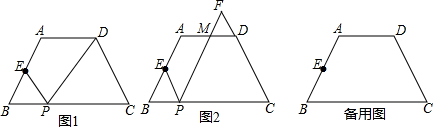
19.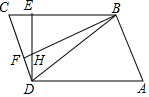 如图,在四边形ABCD中,AB=CD,AB∥CD,DE⊥BC,BF⊥CD,线段DE与BF交于点H.
如图,在四边形ABCD中,AB=CD,AB∥CD,DE⊥BC,BF⊥CD,线段DE与BF交于点H.(1)说明△ABD≌△CDB;
(2)当∠BDE=45°时,说明△BEH≌△DEC.
分析 (1)根据SAS即可证明;
(2)首先证明△BDE是等腰直角三角形,推出BE=DE,由DE⊥BC,BF⊥CD,∠EHB=∠FHD,推出∠CBF=∠CDE,根据ASA即可证明;
解答 解:(1)∵AB∥CD,
∴∠ABD=∠CDB,
△ABD和△CDB中,
$\left\{\begin{array}{l}{AB=CD}\\{∠ABD=∠CDB}\\{BD=BD}\end{array}\right.$,
∴△ABD≌△CDB.
(2)∵∠BDE=45°,DE⊥BC,
∴△BDE是等腰直角三角形,
∴BE=DE,
∵DE⊥BC,BF⊥CD,∠EHB=∠FHD,
∴∠CBF=∠CDE,
在△CDE和△HBE中,
$\left\{\begin{array}{l}{∠BED=∠CED}\\{BE=DE}\\{∠CBF=∠CDE}\end{array}\right.$,
∴△CDE≌△HBE.
点评 本题考查全等三角形的判定和性质、等腰直角三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
10. 小明同学八年级上学期的数学成绩记录如表:
小明同学八年级上学期的数学成绩记录如表:
单位:分
(1)计算小明该学期平时测验的平均成绩;
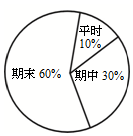
(2)若上学期数学总评成绩按如图(扇形统计图)的权重计算,请求出小明同学该学期的总评成绩.
 小明同学八年级上学期的数学成绩记录如表:
小明同学八年级上学期的数学成绩记录如表:单位:分
| 测验类别 | 平时测验 | 期中考试 | 期末考试 | |||
| 测验1 | 测验2 | 测验3 | 课题学习 | |||
| 成绩 | 88 | 72 | 86 | 98 | 90 | 84 |
(2)若上学期数学总评成绩按如图(扇形统计图)的权重计算,请求出小明同学该学期的总评成绩.
4.下列成语所描述的事件从数学角度看是必然事件的是( )
| A. | 缘木求鱼 | B. | 拔苗助长 | C. | 守株待兔 | D. | 覆水难收 |
11.下列说法正确的是( )
| A. | x没有系数 | B. | π是单项式 | ||
| C. | x4+2x3是七次二项次 | D. | $\frac{3x-1}{5}$是单项式 |