题目内容
20．一次函数的图象与直线y=-x+1平行，且过点（8，2），此一次函数的解析式为（ ）| A． | y=2x-14 | B． | y=-x-6 | C． | y=-x+10 | D． | y=4x |
分析 根据互相平行的直线的解析式的k值相等设出一次函数解析式，再将点（8，2）代入求解即可．
解答 解：∵一次函数的图象与直线y=-x+1平行，
∴设一次函数解析式为y=-x+b，
将（8，2）代入得，-8+b=2，
解得b=10，
所以，一次函数解析式为y=-x+10．
故选C．
点评 本题考查了两直线相交或平行问题，熟记互相平行的直线的解析式的k值相等是解题的关键．
练习册系列答案
相关题目
10．下列各式从左到右的变形中，是因式分解的为（ ）
| A． | a2+b2=（a+b）2 | B． | a2-2ab+b2=（a-b）2 | C． | x2+x3=x3（$\frac{1}{x}$+1） | D． | x（y+z+1）=xy+xz+x |
8．
某校对600名学生进行了一次“心理健康”知识测试，从中抽取了部分学生的成绩（得分取正整数，满分为100分）作为样本，绘制了如图尚未完成的表格和频数分布直方图（注：无50.5以下成绩）
（1）频数分布表中，A=80.5，B=16，C=0.2．
（2）补全频数分布直方图．
（3）若成绩在90分以上（不含90分）为优秀，试估计该校成绩优秀的有多少人？
某校对600名学生进行了一次“心理健康”知识测试，从中抽取了部分学生的成绩（得分取正整数，满分为100分）作为样本，绘制了如图尚未完成的表格和频数分布直方图（注：无50.5以下成绩）| 分组 | 频数 | 频数 |
| 50.5～60.5 | 2 | 0.04 |
| 60.5～70.5 | 8 | 0.16 |
| 70.5～80.5 | 10 | C |
| A～90.5 | B | 0.32 |
| 90.5～100.5 | 14 | 0.28 |
| 合计 |
（2）补全频数分布直方图．
（3）若成绩在90分以上（不含90分）为优秀，试估计该校成绩优秀的有多少人？
5．
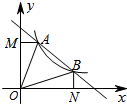如图，已知直线y=-x+b（b＞0）与双曲线y=$\frac{k}{x}$（x＞0）交 于A、B两点，连接OA、OB，AM⊥y轴于点M，BN⊥x轴于点N，下列结论：①OA=OB；②△AOM≌△BON；③当AB=$\sqrt{2}$时，ON=BN=1．④若∠AOB=45°，则S△AOB=k；其中结论正确的是（ ）
如图，已知直线y=-x+b（b＞0）与双曲线y=$\frac{k}{x}$（x＞0）交 于A、B两点，连接OA、OB，AM⊥y轴于点M，BN⊥x轴于点N，下列结论：①OA=OB；②△AOM≌△BON；③当AB=$\sqrt{2}$时，ON=BN=1．④若∠AOB=45°，则S△AOB=k；其中结论正确的是（ ）| A． | ②③ | B． | ①③④ | C． | ①②④ | D． | ①②③④ |
9．用科学记数法表示0.0000039，正确的是（ ）
| A． | 39×10-6 | B． | 3.9×10-6 | C． | 3.9×10-5 | D． | 39×10-5 |
