题目内容
6.如图,在?ABCD中,对角线AC、BD相交于点O,点E在DA的延长线上,连接EB,∠EBD=5∠EDB,∠BCD=90°+$\frac{1}{2}$∠E,过点A作AF⊥BD于点F,若AB=5,则FO的长为$\frac{5}{2}$.
分析 根据已知条件设∠EDB=α,则∠EBD=5α,∠E=180°-∠α,于是得到∠BAD=∠BCD=90°+$\frac{1}{2}$∠E=180°-3α,在BD上取点G,根据等腰三角形的性质得到AG=AB=5,推出AG=GD=5,设BF=FG=5x,得到OB=$\frac{2x+5}{2}$,于是得到结论.
解答 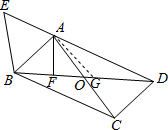 解:设∠EDB=α,则∠EBD=5α,∠E=180°-6α,
解:设∠EDB=α,则∠EBD=5α,∠E=180°-6α,
∴∠BAD=∠BCD=90°+$\frac{1}{2}$∠E=180°-3α,
∴∠EAB=3α,∠ABD=∠EAB-∠EDB=2α,
在BD上取点G,使BF=GF,
∵AF⊥BC,
∴AG=AB=5,∠AGB=∠ABG=2α,
∴∠GAD=α=∠ADB,
∴AG=GD=5,
设BF=FG=x,
∴OB=$\frac{2x+5}{2}$,
∴OF=OB-BF=$\frac{2x+5}{2}$-x=$\frac{5}{2}$.
故答案为:$\frac{5}{2}$.
点评 本题考查了平行四边形的性质,等腰三角形的性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
20.一次函数的图象与直线y=-x+1平行,且过点(8,2),此一次函数的解析式为( )
| A. | y=2x-14 | B. | y=-x-6 | C. | y=-x+10 | D. | y=4x |
18. 如图,已知函数y=$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$的图象与x轴交于点A,与y轴交于点B,点P是x轴上一点,若△PAB为等腰三角形,则点P的坐标不可能是( )
如图,已知函数y=$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$的图象与x轴交于点A,与y轴交于点B,点P是x轴上一点,若△PAB为等腰三角形,则点P的坐标不可能是( )
 如图,已知函数y=$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$的图象与x轴交于点A,与y轴交于点B,点P是x轴上一点,若△PAB为等腰三角形,则点P的坐标不可能是( )
如图,已知函数y=$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$的图象与x轴交于点A,与y轴交于点B,点P是x轴上一点,若△PAB为等腰三角形,则点P的坐标不可能是( )| A. | (-3-2$\sqrt{3}$,0) | B. | (3,0) | C. | (-1,0) | D. | (2$\sqrt{3}$,0) |
15.一次函数y=-3x-6的图象不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
16.若分式$\frac{|b|-3}{{{b^2}-2b-3}}$的值为0,则b的是( )
| A. | 3 | B. | -3 | C. | 1 | D. | ±3 |
