题目内容
15.一个多面体,若顶点数为5,面数为5,则棱数有多少?分析 简单多面体的顶点数V、面数F及棱数E间的关系为:V+F-E=2.这个公式叫欧拉公式.依此即可求解.
解答 解:依题意有
5+5-E=2,
解得E=8.
故棱数有8.
点评 考查了欧拉公式,公式描述了简单多面体顶点数、面数、棱数特有的规律.

练习册系列答案
相关题目
3.有如图所示的几种几何体:

将它们按截面形状分成两类时,下面的分法不正确的是( )

将它们按截面形状分成两类时,下面的分法不正确的是( )
| A. | 截面可能是圆和三角形两类 | B. | 截面可能是圆和四边形两类 | ||
| C. | 截面可能是圆和五边形两类 | D. | 截面可能是三角形和四边形两类 |
4.函数y=$\frac{m(m-3)}{x}$是反比例函数,则m必须满足( )
| A. | m≠3 | B. | m≠0或m≠3 | C. | m≠0 | D. | m≠0且m≠3 |
 如图,在四边形ABCD中,AD∥BC,E、F分别在AB、CD上,AD=2,AB=9,CD=6,BC=7,若EF∥BC,且四边形AEFD与四边形EBCF是周长相等,求EF的长.
如图,在四边形ABCD中,AD∥BC,E、F分别在AB、CD上,AD=2,AB=9,CD=6,BC=7,若EF∥BC,且四边形AEFD与四边形EBCF是周长相等,求EF的长.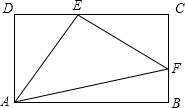 如图,四边形ABCD为矩形,E为CD上一点(不与C、D重合),F为BC上一点(不与C、B重合),△AEF的面积能否达到矩形ABCD面积的一半?请说明理由.
如图,四边形ABCD为矩形,E为CD上一点(不与C、D重合),F为BC上一点(不与C、B重合),△AEF的面积能否达到矩形ABCD面积的一半?请说明理由.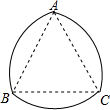 如图所示的图形叫弧三角形,又叫莱洛三角形,是机械学家莱洛首先进行研究的,弧三角形是这样画的:先画正三角形ABC,然后分别以点A,B,C为圆心,AB长为半径画弧,若正三角形ABC的边长为2cm,求弧三角形的周长.
如图所示的图形叫弧三角形,又叫莱洛三角形,是机械学家莱洛首先进行研究的,弧三角形是这样画的:先画正三角形ABC,然后分别以点A,B,C为圆心,AB长为半径画弧,若正三角形ABC的边长为2cm,求弧三角形的周长.