题目内容
8.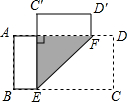 如图,在矩形ABCD中,AB=6cm,点E、F分别是边BC、AD上一点,将矩形ABCD沿EF折叠,使点C、D分别落在点C′、D′处.若C′E⊥AD,则EF的长为6$\sqrt{2}$cm.
如图,在矩形ABCD中,AB=6cm,点E、F分别是边BC、AD上一点,将矩形ABCD沿EF折叠,使点C、D分别落在点C′、D′处.若C′E⊥AD,则EF的长为6$\sqrt{2}$cm.
分析 根据矩形的性质和折叠的性质,由C′E⊥AD,可得四边形ABEG和四边形C′D′FG是矩形,根据矩形的性质可得EG和FG的长,再根据勾股定理可得EF的长.
解答  解:如图所示:
解:如图所示:
∵将矩形ABCD沿EF折叠,使点C、D分别落在点C′、D′处,C′E⊥AD,
∴四边形ABEG和四边形C′D′FG是矩形,
∴EG=FG=AB=6cm,
∴在Rt△EGF中,EF=$\sqrt{E{G}^{2}+F{G}^{2}}$=6$\sqrt{2}$cm.
故答案为:6$\sqrt{2}$cm.
点评 考查了翻折变换(折叠问题),矩形的判定和性质,勾股定理,根据关键是得到EG和FG的长.

练习册系列答案
相关题目
3. 如图,AB∥CD,AD=CD,∠1=70°,则∠2的度数是( )
如图,AB∥CD,AD=CD,∠1=70°,则∠2的度数是( )
 如图,AB∥CD,AD=CD,∠1=70°,则∠2的度数是( )
如图,AB∥CD,AD=CD,∠1=70°,则∠2的度数是( )| A. | 20° | B. | 35° | C. | 40° | D. | 70° |
17.-2的倒数是( )
| A. | -2 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |