题目内容
18.(1)计算:(-1)3-$\sqrt{9}$-12×2-2;(2)解不等式组:$\left\{\begin{array}{l}{2x-1≤3}\\{\frac{x+3}{2}>1}\end{array}\right.$.
分析 (1)原式第一项利用乘方的意义计算,第二项利用算术平方根定义计算,第三项利用负整数指数幂法则计算即可得到结果;
(2)分别求出不等式组中两不等式的解集,找出解集的公共部分即可.
解答 解:(1)原式=-1-3-12×$\frac{1}{4}$=-1-3-3=-7;
(2)$\left\{\begin{array}{l}{2x-1≤3①}\\{\frac{x+3}{2}>1②}\end{array}\right.$,
由①得:x≤2,
由②得:x>-1,
则不等式组的解集为-1<x≤2.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
9. 某地区共有1800名初三学生,为了解这些学生的体质健康状况,开学之初随机选取部分学生进行体育测试,以下是根据测试成绩绘制的统计图表的一部分.
某地区共有1800名初三学生,为了解这些学生的体质健康状况,开学之初随机选取部分学生进行体育测试,以下是根据测试成绩绘制的统计图表的一部分.
根据以上信息,解答下列问题:
(1)本次测试学生体质健康成绩为良好的有36人,达到优秀的人数占本次测试总人数的百分比为70%.
(2)本次测试的学生数为200人,其中,体质健康成绩为及格的有18人,不及格的人数占本次测试总人数的百分比为3%.
(3)试估计该地区初三学生开学之初体质健康成绩达到良好及以上等级的学生数.
 某地区共有1800名初三学生,为了解这些学生的体质健康状况,开学之初随机选取部分学生进行体育测试,以下是根据测试成绩绘制的统计图表的一部分.
某地区共有1800名初三学生,为了解这些学生的体质健康状况,开学之初随机选取部分学生进行体育测试,以下是根据测试成绩绘制的统计图表的一部分.| 等级 | 测试成绩(分) | 人数 |
| 优秀 | 45≤x≤50 | 140 |
| 良好 | 37.5≤x<45 | 36 |
| 及格 | 30≤x<37.5 | |
| 不及格 | x<30 | 6 |
(1)本次测试学生体质健康成绩为良好的有36人,达到优秀的人数占本次测试总人数的百分比为70%.
(2)本次测试的学生数为200人,其中,体质健康成绩为及格的有18人,不及格的人数占本次测试总人数的百分比为3%.
(3)试估计该地区初三学生开学之初体质健康成绩达到良好及以上等级的学生数.
6.有一组数据:1,4,-3,3,4,这组数据的中位数为( )
| A. | -3 | B. | 1 | C. | 3 | D. | 4 |
13. 如图,点P是?ABCD边AB上的一点,射线CP交DA的延长线于点E,则图中相似的三角形有( )
如图,点P是?ABCD边AB上的一点,射线CP交DA的延长线于点E,则图中相似的三角形有( )
 如图,点P是?ABCD边AB上的一点,射线CP交DA的延长线于点E,则图中相似的三角形有( )
如图,点P是?ABCD边AB上的一点,射线CP交DA的延长线于点E,则图中相似的三角形有( )| A. | 0对 | B. | 1对 | C. | 2对 | D. | 3对 |

 由几个相同的小正方形搭成的一个几何体如图所示,这个几何体的主视图是( )
由几个相同的小正方形搭成的一个几何体如图所示,这个几何体的主视图是( )



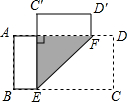 如图,在矩形ABCD中,AB=6cm,点E、F分别是边BC、AD上一点,将矩形ABCD沿EF折叠,使点C、D分别落在点C′、D′处.若C′E⊥AD,则EF的长为6$\sqrt{2}$cm.
如图,在矩形ABCD中,AB=6cm,点E、F分别是边BC、AD上一点,将矩形ABCD沿EF折叠,使点C、D分别落在点C′、D′处.若C′E⊥AD,则EF的长为6$\sqrt{2}$cm.