题目内容
19．某中学要在全校学生中举办“中国梦•我的梦”主题演讲比赛，要求每班选一名代表参赛．九年级（1）班经过投票初选，小亮和小丽票数并列班级第一，现在他们都想代表本班参赛．经班长与他们协商决定，用他们学过的掷骰子游戏来确定谁去参赛（胜者参赛）．规则如下：两人同时随机各掷一枚完全相同且质地均匀的骰子一次，向上一面的点数都是奇数，则小亮胜；向上一面的点数都是偶数，则小丽胜；否则，视为平局，若为平局，继续上述游戏，直至分出胜负为止．
如果小亮和小丽按上述规则各掷一次骰子，那么请你解答下列问题：
（1）小亮掷得向上一面的点数为奇数的概率是多少？
（2）该游戏是否公平？请用列表或树状图等方法说明理由．（骰子：六个面上分别刻有1，2，3，4，5，6个小圆点的小正方体）
分析 （1）首先判断出向上一面的点数为奇数有3种情况，然后根据概率公式，求出小亮掷得向上一面的点数为奇数的概率是多少即可．
（2）首先应用列表法，列举出所有可能的结果，然后分别判断出小亮、小丽获胜的概率是多少，再比较它们的大小，判断出该游戏是否公平即可．
解答 解：（1）∵向上一面的点数为奇数有3种情况，
∴小亮掷得向上一面的点数为奇数的概率是：$\frac{3}{6}=\frac{1}{2}$．
（2）填表如下：
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | （1，1） | （1，2） | （1，3） | （1，4） | （1，5） | （1，6） |
| 2 | （2，1） | （2，2） | （2，3） | （2，4） | （2，5） | （2，6） |
| 3 | （3，1） | （3，2） | （3，3） | （3，4） | （3，5） | （3，6） |
| 4 | （4，1） | （4，2） | （4，3） | （4，4） | （4，5） | （4，6） |
| 5 | （5，1） | （5，2） | （5，3） | （5，4） | （5，5） | （5，6） |
| 6 | （6，1） | （6，2） | （6，3） | （6，4） | （6，5） | （6，6） |
∴P（小亮胜）=$\frac{9}{36}=\frac{1}{4}$，P（小丽胜）=$\frac{9}{36}$=$\frac{1}{4}$，
∴游戏是公平的．
点评 （1）此题主要考查了判断游戏公平性问题，要熟练掌握，首先计算每个事件的概率，然后比较概率的大小，概率相等就公平，否则就不公平．
（2）此题主要考查了列举法（树形图法）求概率问题，解答此类问题的关键在于列举出所有可能的结果，列表法是一种，但当一个事件涉及三个或更多元素时，为不重不漏地列出所有可能的结果，通常采用树形图．
练习册系列答案
能力评价系列答案
唐印文化课时测评系列答案
相关题目
9．
某地区共有1800名初三学生，为了解这些学生的体质健康状况，开学之初随机选取部分学生进行体育测试，以下是根据测试成绩绘制的统计图表的一部分．
根据以上信息，解答下列问题：
（1）本次测试学生体质健康成绩为良好的有36人，达到优秀的人数占本次测试总人数的百分比为70%．
（2）本次测试的学生数为200人，其中，体质健康成绩为及格的有18人，不及格的人数占本次测试总人数的百分比为3%．
（3）试估计该地区初三学生开学之初体质健康成绩达到良好及以上等级的学生数．
某地区共有1800名初三学生，为了解这些学生的体质健康状况，开学之初随机选取部分学生进行体育测试，以下是根据测试成绩绘制的统计图表的一部分．| 等级 | 测试成绩（分） | 人数 |
| 优秀 | 45≤x≤50 | 140 |
| 良好 | 37.5≤x＜45 | 36 |
| 及格 | 30≤x＜37.5 | |
| 不及格 | x＜30 | 6 |
（1）本次测试学生体质健康成绩为良好的有36人，达到优秀的人数占本次测试总人数的百分比为70%．
（2）本次测试的学生数为200人，其中，体质健康成绩为及格的有18人，不及格的人数占本次测试总人数的百分比为3%．
（3）试估计该地区初三学生开学之初体质健康成绩达到良好及以上等级的学生数．
由几个相同的小正方形搭成的一个几何体如图所示，这个几何体的主视图是（ ）
如图，已知△ABC，请用尺规过点A作一条直线，使其将△ABC分成面积相等的两部分．（保留作图痕迹，不写作法）
4．
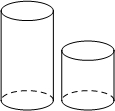图中的两个圆柱体底面半径相同而高度不同，关于这两个圆柱体的视图说法正确的是（ ）
图中的两个圆柱体底面半径相同而高度不同，关于这两个圆柱体的视图说法正确的是（ ）| A． | 主视图相同 | B． | 俯视图相同 | ||
| C． | 左视图相同 | D． | 主视图、俯视图、左视图都相同 |
如图，PA为⊙O的切线，A为切点，B是OP与⊙O的交点．若∠P=20°，OA=3，则$\widehat{AB}$的长为$\frac{7}{6}$π（结果保留π）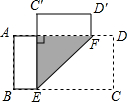
如图，在矩形ABCD中，AB=6cm，点E、F分别是边BC、AD上一点，将矩形ABCD沿EF折叠，使点C、D分别落在点C′、D′处．若C′E⊥AD，则EF的长为6$\sqrt{2}$cm．