题目内容
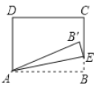
【题目】如图,在矩形![]() 中,
中,![]() 点
点![]() 为射线
为射线![]() 上一动点,将
上一动点,将![]() 沿
沿![]() 折叠,得到
折叠,得到![]() 若
若![]() 恰好落在射线
恰好落在射线![]() 上,则
上,则![]() 的长为________.
的长为________.
【答案】![]() 或15
或15
【解析】
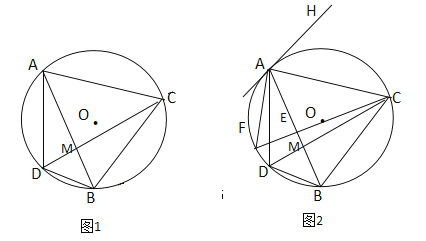
如图1,根据折叠的性质得到AB=A![]() =5,
=5,![]() E=BE,根据勾股定理求出BE,如图2,根据折叠的性质得到A
E=BE,根据勾股定理求出BE,如图2,根据折叠的性质得到A![]() =AB=5,求得AB=BF=5,根据勾股定理得到CF=4根据相似三角形的性质列方程即可得到结论.
=AB=5,求得AB=BF=5,根据勾股定理得到CF=4根据相似三角形的性质列方程即可得到结论.
∵四边形ABCD是矩形,
∴AD=BC=3,CD=AB=5,
如图1,由折叠得AB=A![]() =5,
=5,![]() E=BE,
E=BE,

∴![]() ,
,
∴![]() ,
,
在Rt△![]() 中,
中,![]() ,
,
∴![]() ,
,
解得BE=![]() ;
;
如图2,由折叠得AB=A![]() =5,
=5,

∵CD∥AB,
∴∠![]() =∠
=∠![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵AE垂直平分![]() ,
,
∴BF=AB=5,
∴![]() ,
,
∵CF∥AB,
∴△CEF∽△ABE,
∴![]() ,
,
∴![]() ,
,
∴BE=15,
故答案为:![]() 或15.
或15.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目