Question

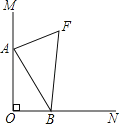
【题目】如图1，已知⊙O是ΔADB的外接圆，∠ADB的平分线DC交AB于点M，交⊙O于点C，连接AC，BC.

（1）求证：AC=BC；

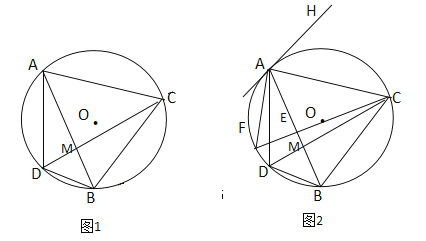
（2）如图2，在图1 的基础上做⊙O的直径CF交AB于点E，连接AF，过点A作⊙O的切线AH，若AH//BC，求∠ACF的度数；

（3）在（2）的条件下，若ΔABD的面积为，ΔABD与ΔABC的面积比为2：9，求CD的长.

Answer 1

【答案】（1）证明见解析；（2）30°；（3）

【解析】

（1）运用“在同圆或等圆中，弧相等，所对的弦相等”可求解；

（2）连接AO并延长交BC于I交⊙O于J,由AH是⊙O的切线且AH∥BC得AI⊥BC，易证∠IAC=30°，故可得∠ABC=60°=∠F=∠ACB，由CF是直径可得∠ACF的度数；

（3）过点D作DG⊥AB ，连接AO，知ABC为等边三角形，求出AB、AE的长，在RtΔAEO中，求出AO的长，得CF的长，再求DG 的长，运用勾股定理易求CD的长.

（1）∵DC平分∠ADB，∴∠ADC=∠BDC， ∴AC=BC．

（2）如图，连接AO并延长交BC于I交⊙O于J

∵AH是⊙O的切线且AH∥BC，

∴AI⊥BC，

∴BI=IC，

∵AC=BC，

∴IC=AC，

∴∠IAC=30°，

∴∠ABC=60°=∠F=∠ACB．

∵FC是直径，

∴∠FAC=90°，

∴∠ACF=180°-90°-60°=30°．

（3）过点D作，连接AO

由（1）（2）知ABC为等边三角形

∵∠ACF=30°，

∴，

∴AE=BE，

∴，

∴AB=，

∴．

在RtΔAEO中，设EO=x，则AO=2x，

∴，

∴，

∴x=6，⊙O的半径为6，

∴CF=12．

∵，

∴DG=2．

如图，过点D作,连接OD．

∵,，

∴CF//DG，

∴四边形G′DGE为矩形，

∴，

，

在RtΔ中，，

∴，

∴