题目内容
10.已知等边△ABC的两个顶点的坐标为A(0,4),B(0,-2),则点C的坐标为(3$\sqrt{3}$,1)或(-3$\sqrt{3}$,1).分析 作CH⊥AB于H,根据点A和B的坐标,得AB=6.根据等腰三角形的三线合一的性质,得AH=BH=3,再根据勾股定理求得CH=3$\sqrt{3}$,从而写出点C的坐标.
解答 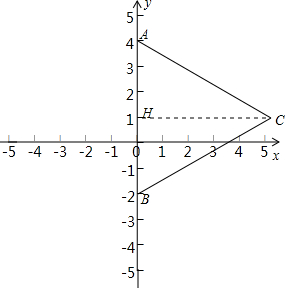 解:作CH⊥AB于H.
解:作CH⊥AB于H.
∵A(0,4),B(0,-2),
∴AB=6.
∵△ABC是等边三角形,
∴AH=BH=3,
AC=AB=6,
∴CH=$\sqrt{A{C}^{2}-A{H}^{2}}$=3$\sqrt{3}$,
OH=1,
∴C(3$\sqrt{3}$,1);
同理,当点C在第三象限时,C(-3$\sqrt{3}$,1).
故答案为:(3$\sqrt{3}$,1)或(-3$\sqrt{3}$,1).
点评 此题考查了等边三角形的性质,用到的知识点是勾股定理、坐标与图形的性质,关键是根据题意画出图形,不要漏解.

练习册系列答案
相关题目
18.如果2x3myn+4与-3x9y3n是同类项,那么m、n的值分别为( )
| A. | m=-2,n=3 | B. | m=2,n=3 | C. | m=3,n=2 | D. | m=3,n=2 |
 如图,∠1=70°,∠2=130°,直线m平移后得到直线n,则∠3=20°.
如图,∠1=70°,∠2=130°,直线m平移后得到直线n,则∠3=20°.
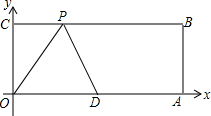 如图,O为坐标原点,四边形OABC为长方形,边OA和OC分别落在x轴和y轴的正半轴上,且A(10,0),C(0,4),点D是OA的中点,点P在线段BC上运动,当△ODP为腰长为5的等腰三角形时,求点P的坐标.
如图,O为坐标原点,四边形OABC为长方形,边OA和OC分别落在x轴和y轴的正半轴上,且A(10,0),C(0,4),点D是OA的中点,点P在线段BC上运动,当△ODP为腰长为5的等腰三角形时,求点P的坐标.