题目内容
9.已知|a+1|+(b-2)2=0,则(a+b)2011的值为( )| A. | 2011 | B. | 1 | C. | -1 | D. | 0 |
分析 根据|a+1|+(b-2)2=0,可得a+1=0,b-2=0,求出a、b的值各是多少,即可求出(a+b)2011的值为多少.
解答 解:∵|a+1|+(b-2)2=0,
∴a+1=0,b-2=0,
解得a=-1,b=2,
∴(a+b)2011=(-1+2)2011=1.
故选:B.
点评 此题主要考查了代数式求值问题,要熟练掌握,求代数式的值可以直接代入、计算.如果给出的代数式可以化简,要先化简再求值.题型简单总结以下三种:①已知条件不化简,所给代数式化简;②已知条件化简,所给代数式不化简;③已知条件和所给代数式都要化简.

练习册系列答案
相关题目
17.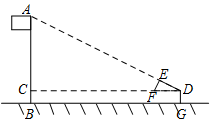 如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一直线上,已知DE=0.5米,EF=0.25米,目测点D到地面的距离DG=1.5米,到旗杆的水平距离DC=20米,则旗杆的高度为( )
如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一直线上,已知DE=0.5米,EF=0.25米,目测点D到地面的距离DG=1.5米,到旗杆的水平距离DC=20米,则旗杆的高度为( )
 如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一直线上,已知DE=0.5米,EF=0.25米,目测点D到地面的距离DG=1.5米,到旗杆的水平距离DC=20米,则旗杆的高度为( )
如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一直线上,已知DE=0.5米,EF=0.25米,目测点D到地面的距离DG=1.5米,到旗杆的水平距离DC=20米,则旗杆的高度为( )| A. | 10$\sqrt{5}$米 | B. | (10$\sqrt{5}$+1.5)米 | C. | 11.5米 | D. | 10米 |
14.下列各图案中是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
1. 如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为($\frac{1}{2}$,1),下列结论:①abc<0;②a+b=0;③4ac-b2=4a;④a+b+c<0.其中正确的有( )个.
如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为($\frac{1}{2}$,1),下列结论:①abc<0;②a+b=0;③4ac-b2=4a;④a+b+c<0.其中正确的有( )个.
 如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为($\frac{1}{2}$,1),下列结论:①abc<0;②a+b=0;③4ac-b2=4a;④a+b+c<0.其中正确的有( )个.
如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为($\frac{1}{2}$,1),下列结论:①abc<0;②a+b=0;③4ac-b2=4a;④a+b+c<0.其中正确的有( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
18.在下列各数中,无理数是( )
| A. | $\sqrt{4}$ | B. | 3π | C. | $\frac{22}{7}$ | D. | $\root{3}{8}$ |
9.如果一个数的平方根与立方根相同,那么这个数是( )
| A. | 0 | B. | ±1 | C. | 0和1 | D. | 0 或±1 |



