题目内容
如图，已知△ABC中，∠ACB=90°．（1）利用尺规作图，作一个点P，使得点P到∠ACB两边的距离相等，且PA=PB；
（2）试判断△ABP的形状，并说明理由．
考点：作图—复杂作图,角平分线的性质,线段垂直平分线的性质,等腰直角三角形
专题：
分析：（1）作∠ACB的角平分线，再作AB的垂直平分线，两线的交点就是P点位置；
（2）根据角平分线性质和线段垂直平分线的性质可得∠PAC=∠PBC=90°，再根据四边形内角和定理可得∠APB=90°，进而得到△ABP的形状．
（2）根据角平分线性质和线段垂直平分线的性质可得∠PAC=∠PBC=90°，再根据四边形内角和定理可得∠APB=90°，进而得到△ABP的形状．
解答：
解：（1）如图所示：
（2）∵CP平分∠ACB，PA=PB，
∴∠PAC=∠PBC=90°，
∴∠APB=360°-90°-90°-90°=90°，
∴△APB是等腰直角三角形．
解：（1）如图所示：（2）∵CP平分∠ACB，PA=PB，
∴∠PAC=∠PBC=90°，
∴∠APB=360°-90°-90°-90°=90°，
∴△APB是等腰直角三角形．
点评：此题主要考查了复杂作图，关键是掌握角平分线的性质和线段垂直平分线的性质．
练习册系列答案
寒假天地重庆出版社系列答案
相关题目
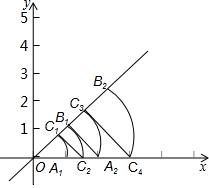如图，已知直线l的表达式为y=x，点A1的坐标为（1，0），以O为圆心，OA1为半径画弧，与直线l交于点C1，记
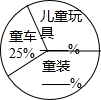“六•一”快到了，质检部门从某超市经销的儿童玩具、童车和童装中共抽查了300件儿童用品．图4是根据抽查结果绘制出的不完整的统计表和扇形图，请根据统计表和扇形图提供的信息，完成下列问题：
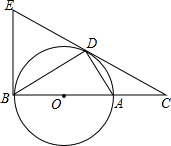如图，AB是⊙O 直径，点C在其延长线上，D为⊙O上一点，且∠CDA=∠CBD．