题目内容
在△ABC中,∠A=80°,若O为外心,则∠BOC= °;若I为内心,则∠BIC= °.
考点:三角形的内切圆与内心,三角形的外接圆与外心
专题:
分析:根据题意画出图形,根据圆周角定理求出即可,再根据题意,求出∠IBC+∠ICB度数,根据三角形内角和定理即可求出∠BIC.
解答: 解:如图1所示:
解:如图1所示:
∵∠A=80°,O为外心,
则∠BOC=160°,
如图2,∵∠A+∠ABC+∠ACB=180°,∠A=80°,
∴∠ABC+∠ACB=100°,
∵I是△ABC的内心,
 ∴∠IBC=
∴∠IBC=
∠ABC,∠ICB=
∠ACB,
∴∠IBC+∠ICB=
×100°=50°,
∴∠BIC=180°-(∠IBC+∠ICB)=130°;
故答案为:160,130.
 解:如图1所示:
解:如图1所示:∵∠A=80°,O为外心,
则∠BOC=160°,
如图2,∵∠A+∠ABC+∠ACB=180°,∠A=80°,
∴∠ABC+∠ACB=100°,
∵I是△ABC的内心,
 ∴∠IBC=
∴∠IBC=| 1 |
| 2 |
| 1 |
| 2 |
∴∠IBC+∠ICB=
| 1 |
| 2 |
∴∠BIC=180°-(∠IBC+∠ICB)=130°;
故答案为:160,130.
点评:本题考查了圆周角定理,三角形的内切圆和外接圆的应用,注意:同弧或等弧所对圆周角等于它所对圆心角的一半.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列四个图案中,既是轴对称图形又是中心对称图形的有( )
A、 |
B、 |
C、 |
D、 |
 如图,已知△ABC中,∠ACB=90°.
如图,已知△ABC中,∠ACB=90°. 甲、乙两车同时从A地出发,以各自的速度匀速向B地行驶.甲车先到达B地后,立即按原路以相同速度匀速返回(停留时间不作考虑),直到两车相遇.若甲、乙两车之间的距离y(千米)与两车行驶的时间x(小时)之间的函数图象如图所示,则A、B两地之间的距离为
甲、乙两车同时从A地出发,以各自的速度匀速向B地行驶.甲车先到达B地后,立即按原路以相同速度匀速返回(停留时间不作考虑),直到两车相遇.若甲、乙两车之间的距离y(千米)与两车行驶的时间x(小时)之间的函数图象如图所示,则A、B两地之间的距离为 将一个有45°角的三角板的直角顶点C放在一张宽为5cm的纸带边沿上.另一个顶点B在纸带的另一边沿上,测得∠DBC=30°,则三角板的最大边的长为
将一个有45°角的三角板的直角顶点C放在一张宽为5cm的纸带边沿上.另一个顶点B在纸带的另一边沿上,测得∠DBC=30°,则三角板的最大边的长为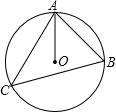 如图,⊙O是△ABC的外接圆,已知∠B=58°,则∠CAO的度数是
如图,⊙O是△ABC的外接圆,已知∠B=58°,则∠CAO的度数是 如图,⊙O的直径CD经过弦EF的中点G,∠DCF=20°,则∠EOD等于
如图,⊙O的直径CD经过弦EF的中点G,∠DCF=20°,则∠EOD等于