题目内容
5.已知关于x的方程x2-mx-3x+m-4=0(m为常数).(1)求证:方程有两个不相等的实数根;
(2)设x1,x2是方程的两个实数根,且x1+x2=6.请求出方程的这两个实数根.
分析 (1)根据根的判别式△=(-m-3)2-4(m-4)=m2+2m+25=(m+1)2+24,证明△>0,即方程有两个不相等的实数根;
(2)首先根据x1+x2=6求出m的值,然后根据公式法求出方程的两个根.
解答 (1)证明:∵关于x的方程x2-mx-3x+m-4=0(m为常数),
∴此方程为x2-(m+3)x+m-4=0,
∴△=(-m-3)2-4(m-4)=m2+2m+25=(m+1)2+24,
∴△>0,
∴关于x的方程x2-mx-3x+m-4=0有两个不相等的实数根;
(2)解:∵x1,x2是方程的两个实数根,
∴x1+x2=m+3,x1•x2=m-4,
∵x1+x2=6,
∴m+3=6,
∴m=3,
∴原一元二次方程为:x2-6x-1=0,
解得x1=3$+\sqrt{10}$,x2=$3-\sqrt{10}$,
∴此方程两根分别为:x1=3$+\sqrt{10}$,x2=$3-\sqrt{10}$.
点评 本题主要考查了根的判别式与根与系数的关系的知识,解答本题的关键是掌握一元二次方程ax2+bx+c=0有两个不相等的根,则根的判别式△>0,此题还要掌握公式法解一元二次方程,此题难度不大.

练习册系列答案
相关题目
10.现有四根长3cm、4cm、7cm、9cm的木棒,任取其中的三根,首尾相连后,能组成三角形的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}$ |
17.下列各式中能用完全平方公式分解因式的是( )
| A. | a2+2ax+4x2 | B. | -a2-4ax+4x2 | C. | -2x+1+4x2 | D. | x4+4+4x2 |
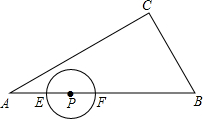 如图,在Rt△ABC中,∠C=90°,BC=3,∠A=30°,点P在AB上,AP=2.点E、F同时从点P出发,分别沿PA、PB以每秒1个单位长度的速度向点A、B匀速运动,点E到达点A后立刻以原速度沿AB向点B运动,点F运动到点B时停止,点E也运动到点B时停止.在点E、F运动过程中,以EF为直径作圆.设点E运动的时间为t秒.
如图,在Rt△ABC中,∠C=90°,BC=3,∠A=30°,点P在AB上,AP=2.点E、F同时从点P出发,分别沿PA、PB以每秒1个单位长度的速度向点A、B匀速运动,点E到达点A后立刻以原速度沿AB向点B运动,点F运动到点B时停止,点E也运动到点B时停止.在点E、F运动过程中,以EF为直径作圆.设点E运动的时间为t秒.