题目内容
20.在Rt△ABC中,∠C=90°,CB=8cm,若斜边AB的垂直平分线交CB于点D,CD=2cm,则AD=6cm.分析 首先根据题意画出图形,然后由CB=8cm,CD=2cm,可求得BD的长,又由斜边AB的垂直平分线交CB于点D,根据线段垂直平分线的性质,可求得AD的长.
解答  解:如图,∵CB=8cm,CD=2cm,
解:如图,∵CB=8cm,CD=2cm,
∴BD=CB-C=8-2=6(cm),
∵斜边AB的垂直平分线交CB于点D,
∴AD=BD=6cm.
故答案为:6.
点评 此题考查了线段垂直平分线的性质.注意垂直平分线上任意一点,到线段两端点的距离相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.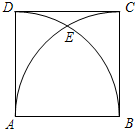 如图,正方形ABCD的边长AB=4,分别以点A、B为圆心,AB长为半径画弧,两弧交于点E,则CE弧的长是( )
如图,正方形ABCD的边长AB=4,分别以点A、B为圆心,AB长为半径画弧,两弧交于点E,则CE弧的长是( )
 如图,正方形ABCD的边长AB=4,分别以点A、B为圆心,AB长为半径画弧,两弧交于点E,则CE弧的长是( )
如图,正方形ABCD的边长AB=4,分别以点A、B为圆心,AB长为半径画弧,两弧交于点E,则CE弧的长是( )| A. | $\frac{2}{3}π$ | B. | π | C. | $\frac{4}{3}π$ | D. | $\frac{8}{3}π$ |
10.$\frac{2}{3}$的倒数是( )
| A. | $\frac{2}{3}$ | B. | -$\frac{2}{3}$ | C. | -$\frac{3}{2}$ | D. | $\frac{3}{2}$ |
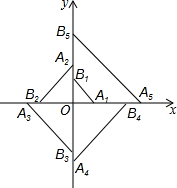 如图,已知腰长为1的等腰直角三角形OA1B1的斜边A1B1在第一象限(顶点A1、B1在坐标轴上),以A1B1的长为腰作等腰直角三角形OA2B2,使斜边A2B2在第二象限(顶点A2、B2在坐标轴上),以A2B2的长为腰作等腰直角三角形OA3B3,使斜边A3B3在第三象限(顶点A3、B3在坐标轴上),…按如图的方式依次作下去,则A2015B2015的中点M2015的坐标是(-21006,-21006).
如图,已知腰长为1的等腰直角三角形OA1B1的斜边A1B1在第一象限(顶点A1、B1在坐标轴上),以A1B1的长为腰作等腰直角三角形OA2B2,使斜边A2B2在第二象限(顶点A2、B2在坐标轴上),以A2B2的长为腰作等腰直角三角形OA3B3,使斜边A3B3在第三象限(顶点A3、B3在坐标轴上),…按如图的方式依次作下去,则A2015B2015的中点M2015的坐标是(-21006,-21006). 如图,直线PQ与⊙O相交于点A、B,BC是⊙O的直径,BD平分∠CBQ交⊙O于点D,过点D作DE⊥PQ,垂足为E.
如图,直线PQ与⊙O相交于点A、B,BC是⊙O的直径,BD平分∠CBQ交⊙O于点D,过点D作DE⊥PQ,垂足为E.