题目内容
观察下列运算:81=8,82=64,83=512,84=4096,85=32768,86=262144,…,则:81+82+83+84+…+82015的个位数字是( )
| A、2 | B、4 | C、6 | D、8 |
考点:尾数特征
专题:
分析:易得底数为8的幂的个位数字依次为8,4,2,6,以4个为周期,个位数字相加为0,成周期性循环.那么让2015除以4看余数是几,得到相和的个位数字即可.
解答:解:2015÷4=503…3,
循环了503次,还有3个个位数字为8,4,2,
所以81+82+83+84+…+82015的和的个位数字是503×0+8+4+2=14.
故81+82+83+84+…+82015的个位数字是4.
故选:B.
循环了503次,还有3个个位数字为8,4,2,
所以81+82+83+84+…+82015的和的个位数字是503×0+8+4+2=14.
故81+82+83+84+…+82015的个位数字是4.
故选:B.
点评:本题主要考查了数字的变化类-尾数的特征,得到底数为8的幂的个位数字的循环规律是解决本题的突破点.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
 函数y=ax2+bx+c的图象的右侧如图所示,下列选项不正确的是( )
函数y=ax2+bx+c的图象的右侧如图所示,下列选项不正确的是( )| A、a>0 | B、c>0 |
| C、b>0 | D、a+b-c>0 |
 一个滑轮起重装置如图所示,假设绳索与滑轮之间没有滑动,滑轮的一条半径OA绕轴心O按逆时针方向旋转的角度为54°,此时重物上升3πcm,滑轮的半径是( )
一个滑轮起重装置如图所示,假设绳索与滑轮之间没有滑动,滑轮的一条半径OA绕轴心O按逆时针方向旋转的角度为54°,此时重物上升3πcm,滑轮的半径是( )| A、5cm | B、10cm |
| C、15cm | D、20cm |
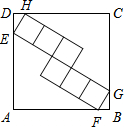 如图,正方形ABCD的边长为5,内部有6个大小相同的小正方形,小正方形的顶点E、F、G、H分别落在边AD、AB、BC、CD上,则小正方形的边长为
如图,正方形ABCD的边长为5,内部有6个大小相同的小正方形,小正方形的顶点E、F、G、H分别落在边AD、AB、BC、CD上,则小正方形的边长为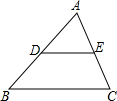 如图,已知DE∥BC,且∠ADE=62°,∠DEC=112°,则∠B=
如图,已知DE∥BC,且∠ADE=62°,∠DEC=112°,则∠B= 在边长为1的小正方形网格中(如图),△AOB的顶点均在格点上
在边长为1的小正方形网格中(如图),△AOB的顶点均在格点上