题目内容
用长为20cm的线段围成一个面积最大的扇形,此时扇形的面积为 cm2.
考点:扇形面积的计算
专题:
分析:设扇形的半径为r,弧长为l,根据扇形的面积公式列出关与S与r的表达式,求出S的最大值即可.
解答:解:设扇形的半径为r,弧长为l,
∵l+2r=20,
∴l=20-2r,
∴S=
lr=
×(20-2r)×r=-(r-5)2+25,
∴S最大=25cm2.
故答案为:25.
∵l+2r=20,
∴l=20-2r,
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
∴S最大=25cm2.
故答案为:25.
点评:本题考查的是扇形面积的计算,熟记扇形的面积公式是解答此题的关键.

练习册系列答案
相关题目
发射一枚炮弹,经x秒后的高度为y公尺,且时间与高度关系为y=ax2+bx,若此炮弹在第10秒与第20秒时的高度相等,则下列四个时间中,哪一个时间炮弹的高度是最高的?( )
| A、第9秒 | B、第13秒 |
| C、第15秒 | D、第18秒 |
在-3、2、0、-1这四个数中,最小的数是( )
| A、-3 | B、-1 | C、0 | D、2 |
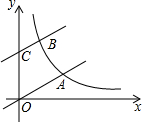 如图,直线y=
如图,直线y=| 1 |
| 2 |
| k |
| x |
| 1 |
| 2 |
| k |
| x |
| A、(2,3) | ||||
| B、(2,4) | ||||
C、(1,
| ||||
D、(
|
 如图,⊙O与射线AM相切于点B,圆心O在射线AN上,⊙O半径为6cm,OA=10cm.点P从点A出发,以2cm/秒的速度沿AN方向运动,过P点作直线l垂直AB,当l与⊙O相切时,所用时间是( )
如图,⊙O与射线AM相切于点B,圆心O在射线AN上,⊙O半径为6cm,OA=10cm.点P从点A出发,以2cm/秒的速度沿AN方向运动,过P点作直线l垂直AB,当l与⊙O相切时,所用时间是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列算式中,错误的是( )
| A、1-1=1 |
| B、(-π-3)0=1 |
| C、(-2)-2=0.25 |
| D、0-3=0 |
 如图,C是线段AB的中点,D是AC的中点,已知所有线段的长度长度之和为13,求AC的长.
如图,C是线段AB的中点,D是AC的中点,已知所有线段的长度长度之和为13,求AC的长.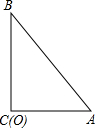 如图,在Rt△ABC中,∠C=90°,AC=10,BC=24,⊙O的半径为6,当圆心O与C重合时,试判断⊙O与AB的位置关系.
如图,在Rt△ABC中,∠C=90°,AC=10,BC=24,⊙O的半径为6,当圆心O与C重合时,试判断⊙O与AB的位置关系.