题目内容
16.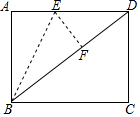 如图,在矩形ABCD中BC=8,CD=6,将△ABE沿BE折叠,使点A恰好落在对角线BD上F处,则DE的长是( )
如图,在矩形ABCD中BC=8,CD=6,将△ABE沿BE折叠,使点A恰好落在对角线BD上F处,则DE的长是( )| A. | 3 | B. | $\frac{24}{5}$ | C. | 5 | D. | $\frac{89}{16}$ |
分析 由ABCD为矩形,得到∠BAD为直角,且三角形BEF与三角形BAE全等,利用全等三角形对应角、对应边相等得到EF⊥BD,AE=EF,AB=BF,利用勾股定理求出BD的长,由BD-BF求出DF的长,在Rt△EDF中,设EF=x,表示出ED,利用勾股定理列出关于x的方程,求出方程的解得到x的值,即可确定出DE的长.
解答 解:∵矩形ABCD,
∴∠BAD=90°,
由折叠可得△BEF≌△BAE,
∴EF⊥BD,AE=EF,AB=BF,
在Rt△ABD中,AB=CD=6,BC=AD=8,
根据勾股定理得:BD=10,即FD=10-6=4,
设EF=AE=x,则有ED=8-x,
根据勾股定理得:x2+42=(8-x)2,
解得:x=3(负值舍去),
则DE=8-3=5,
故选C
点评 此题考查了翻折变换,矩形的性质,以及勾股定理,熟练掌握定理及性质是解本题的关键.

练习册系列答案
相关题目
6.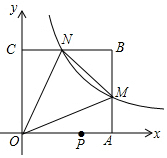 如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点.△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )
如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点.△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )
 如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点.△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )
如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点.△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )| A. | 6$\sqrt{2}$ | B. | 10 | C. | 2$\sqrt{26}$ | D. | 2$\sqrt{29}$ |
7. 如图的几何体由五个相同的小正方体搭成,它的主视图是( )
如图的几何体由五个相同的小正方体搭成,它的主视图是( )
 如图的几何体由五个相同的小正方体搭成,它的主视图是( )
如图的几何体由五个相同的小正方体搭成,它的主视图是( )| A. |  | B. |  | C. |  | D. |  |
19.利用数学计算器求一组数据的平均数,其按键顺序如下:

则输出结果为( )

则输出结果为( )
| A. | 1.5 | B. | 6.75 | C. | 2 | D. | 7 |