题目内容
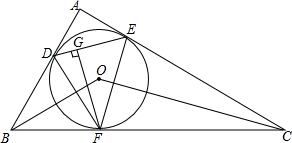 如图,△ABC的三边与其内切圆分别切于D、E、F三点,在△DEF中,作FG⊥DE,连结OB、OF、OC.求证:DG•CF=EG•BF.
如图,△ABC的三边与其内切圆分别切于D、E、F三点,在△DEF中,作FG⊥DE,连结OB、OF、OC.求证:DG•CF=EG•BF.考点:三角形的内切圆与内心,相似三角形的判定与性质
专题:证明题
分析:连结OF,OE,OD,如图,根据切线的性质得OF⊥BC,根据切线长定理得CE=CF,而OE=OF,则OC垂直平分EF,所以OC平分∠EOF,即∠FOC=
∠EOF,利用圆周角定理得∠FDG=
∠EOF,所以∠FOC=∠GDF,于是可证明Rt△GDF∽Rt△FOC,得到DG:OF=FG:CF,变形得DG•CF=OF•FG,同理可得Rt△GEF∽Rt△FOB,得到EG:OF=FG:BF,变形得EG•BF=OF•FG,所以DG•CF=EG•BF.
| 1 |
| 2 |
| 1 |
| 2 |
解答:证明:连结OF、OE、OD,如图,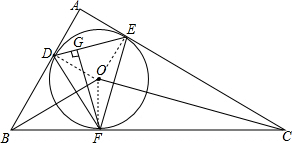
∵△ABC的三边与其内切圆分别切于D、E、F三点,
∴OF⊥BC,CE=CF,
∴∠OFC=∠OFB=90°,
∵OE=OF,
∴OC垂直平分EF,
∴OC平分∠EOF,
∴∠FOC=
∠EOF,
∵∠FDG=
∠EOF,
∴∠FOC=∠GDF,
∵FG⊥DE,
∴∠GDF=90°,
∴Rt△GDF∽Rt△FOC,
∴DG:OF=FG:CF,
∴DG•CF=OF•FG,
同理可得Rt△GEF∽Rt△FOB,
∴EG:OF=FG:BF,
∴EG•BF=OF•FG,
∴DG•CF=EG•BF.

∵△ABC的三边与其内切圆分别切于D、E、F三点,
∴OF⊥BC,CE=CF,
∴∠OFC=∠OFB=90°,
∵OE=OF,
∴OC垂直平分EF,
∴OC平分∠EOF,
∴∠FOC=
| 1 |
| 2 |
∵∠FDG=
| 1 |
| 2 |
∴∠FOC=∠GDF,
∵FG⊥DE,
∴∠GDF=90°,
∴Rt△GDF∽Rt△FOC,
∴DG:OF=FG:CF,
∴DG•CF=OF•FG,
同理可得Rt△GEF∽Rt△FOB,
∴EG:OF=FG:BF,
∴EG•BF=OF•FG,
∴DG•CF=EG•BF.
点评:本题考查了三角形的内切圆和内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.三角形的内心就是三角形三个内角角平分线的交点.也考查了相似三角形的判定与性质.

练习册系列答案
相关题目
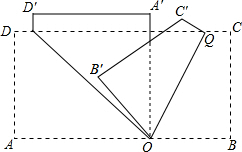 要用一张长方形纸折成一个纸袋,两条折痕的夹角为70°(即∠POQ=70°),将折过来的重叠部分抹上胶水,即可做成一个纸袋,则粘胶水部分所构成的角,∠A′OB′=
要用一张长方形纸折成一个纸袋,两条折痕的夹角为70°(即∠POQ=70°),将折过来的重叠部分抹上胶水,即可做成一个纸袋,则粘胶水部分所构成的角,∠A′OB′=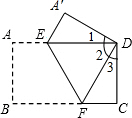 把一个长方形(对边平行且相等,每一个角均为直角)纸片按图进行折叠,使顶点B和D重合,折痕为EF.请问△A′ED与△CFD全等吗?若全等,请证明.
把一个长方形(对边平行且相等,每一个角均为直角)纸片按图进行折叠,使顶点B和D重合,折痕为EF.请问△A′ED与△CFD全等吗?若全等,请证明. 如图,在△ABC中,AB=AC,点D(不与点B重合)在BC上,点E是AB的中点,过点A作AF∥BC交DE延长线于点F,连接AD,BF.
如图,在△ABC中,AB=AC,点D(不与点B重合)在BC上,点E是AB的中点,过点A作AF∥BC交DE延长线于点F,连接AD,BF. 如图是一座抛物线形拱桥,正常水位时桥下水面宽度为20m,拱顶距离水面4m,在图中直角坐标系中该抛物丝的解析式.
如图是一座抛物线形拱桥,正常水位时桥下水面宽度为20m,拱顶距离水面4m,在图中直角坐标系中该抛物丝的解析式.